Закон больших чисел в форме Чебышева.

Если явление устойчивости средних имеет место в действительности, то в математической модели, с помощью которой мы изучаем случайные явления, должна существовать отражающая этот факт теорема. В условиях этой теоремы введем ограничения на случайные величины :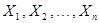

а) Каждая случайная величина имеет математическое ожидание

M( ) , .

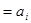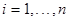б) Дисперсии ограничены одним и тем же числом, т.е.

D( )<C, .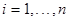

в) Случайные величины попарно независимы, т.е. любые две и 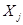при i¹j независимы. Тогда, очевидно

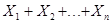D( 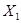)=D( )+D( 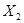)+...+D( ).

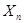Сформулируем закон больших чисел в форме Чебышева.

Теорема. Если для случайных величин 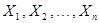выполняются условия а) - в), то для любого 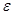>0 имеем при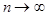

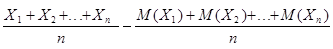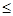
P{|| 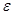}®1.

Доказательство. Пусть

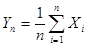, тогда M() = ,

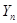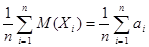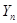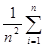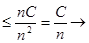D( ) = D( ) 0.

Величина 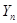удовлетворяет всем требованиям для применения неравенства Чебышева, а именно, при любом 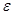>0

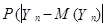
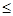
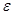)®1,

что и требовалось доказать.

Следствие. Если M( 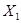) = ... =M( 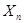) 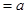, то для любого 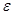>0 при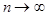

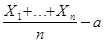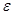P{| ½< }®1.

Отсюда видно, что среднее арифметическое значение случайных величин - случайная величина, при большом числе n сколь угодно мало отличается от постоянной 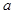, т.е. утрачивает случайный характер.

Смысл з.б.ч. заключается, грубо говоря, в том, что при осреднении большого числа n случайных слагаемых все менее ощущается характерный для случайной величины неконтролируемый разброс в их значениях, так что в пределе по 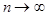этот разброс исчезает вовсе или, как принято говорить, случайная величина вырождается в неслучайную. Однако при любом конечном числе слагаемых n случайный разброс у среднего арифметического этих слагаемых остается. Поэтому возникает вопрос исследования (при 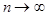) характера этого разброса. Фундаментальный результат в этом направлении (известный как “центральная предельная теорема” ) был впервые сформулирован Лапласом (см. §5.2).