Закон больших чисел в форме Бернулли.

Хотя в основе любого статистического вывода лежит понятие вероятности, мы лишь в немногих случаях можем определить вероятность события непосредственно. Иногда эту вероятность можно установить из соображений симметрии, равной возможности и т.п. (см. тему 2), но универсального метода, который позволял бы для произвольного события указать его вероятность, не существует. Теорема Бернулли дает возможность приближенной оценки вероятности, если для интересующего нас события А можно проводить повторные независимые испытания (см. схема Бернулли и статистическое определение вероятности). Она устанавливает связь между относительной частотой события и его вероятностью. При неограниченном увеличении числа независимых испытаний относительная частота 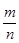некоторого события А сходится по вероятности к вероятности p =Р(А).

Теорема Бернулли. Пусть производится n независимых испытаний, в каждом из которых вероятность p появления события А постоянна, т.е. Р(А) = p. Тогда, если число испытаний достаточно велико ( 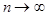), то как угодно близка к единице вероятность того, что отклонение относительной частоты 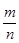от вероятности p по абсолютной величине будет сколь угодно малым, т.е.

P(½ 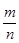- p ½< 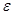)®1.

Доказательство. Применим теорему Чебышева. Пусть – число появлений события А в i – ом испытании, i = 1, 2, . . . , n . Каждая из величин может принять лишь два значения:

= 1 ( событие А наступило ) с вероятностью p ,

= 0 ( событие А не наступило ) с вероятностью q = 1– p .

Пусть 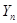= 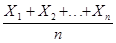. Сумма 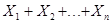равна числу m появлений события А в n испытаниях ( 0 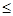m 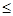n ) , а, значит, 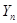= 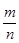– относительная частота появления события А в n испытаниях . Математическое ожидание и дисперсия равны соответственно : M( ) = p , D( )= pq ( см. Математическое ожидание, дисперсия и их свойства ) .

M( 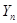)= = 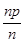p , D( 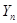) = 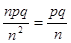® 0 , так как pq – ограничено величиной 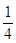. Следовательно, выполняются условия теоремы Чебышева, т.е.

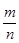P(½ - p ½ 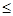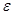)®1 при 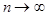, что и требовалось доказать.