Ковариация и коэффициент корреляции.
Между случайными величинами может существовать функциональная или стохастическая (вероятностная) зависимость. Стохастическая зависимость проявляется в том, что условный закон распределения одной случайной величины изменяется в зависимости от значений, принимаемых другой случайной величиной. Одной из характеристик стохастической зависимости двух случайных величин является ковариация случайных величин.
Ковариацией случайных величин (X,Y) называется число 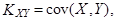 равное математическому ожиданию произведения отклонений случайных величин X и Y от своих математических ожиданий:
равное математическому ожиданию произведения отклонений случайных величин X и Y от своих математических ожиданий:
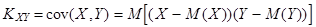 .
.
Иногда ковариацию называют корреляционным моментом или вторым смешанным центральным моментом случайных величин (X,Y).
Используя определение математического ожидания, получим:
для дискретного распределения
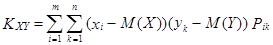 ,
,
для непрерывного распределения
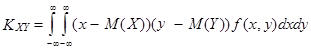 .
.
При Y = X ковариация совпадает с дисперсией Х.
Величина корреляционного момента зависит от единиц измерения случайных величин. Это затрудняет сравнение корреляционных моментов различных систем случайных величин. Для устранения этого недостатка вводится новая числовая характеристика – коэффициент корреляции 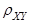 , который является
, который является
безразмерной величиной.
Для его вычисления заменим отклонения случайных величин от математических ожиданий их нормированными отклонениями, т.е.
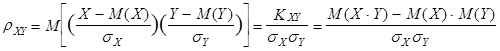 .
.
Свойства коэффициента корреляции:
1. 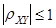
Пусть t – переменная величина в смысле математического анализа. Рассмотрим дисперсию случайной величины D(Y – tX) как функцию переменной t .
По свойству дисперсии 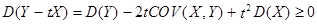 . Дискриминант в этом случае должен быть меньше либо равен нулю, т.е.
. Дискриминант в этом случае должен быть меньше либо равен нулю, т.е.
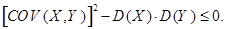 , откуда получим
, откуда получим
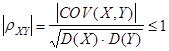
2. Модуль коэффициента корреляции не меняется при линейных преобразованиях случайных переменных: 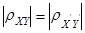 , где
, где 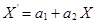 ,
, 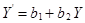 ,
, 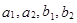 – произвольные числа.
– произвольные числа.
3. 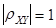 , тогда и только тогда, когда случайные величины X и Y связаны линейно, т.е. существуют такие числа a, b, что
, тогда и только тогда, когда случайные величины X и Y связаны линейно, т.е. существуют такие числа a, b, что 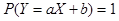 .
.
Если 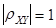 , то рассматриваемый в п.1 дискриминант равен нулю, а поэтому при некотором
, то рассматриваемый в п.1 дискриминант равен нулю, а поэтому при некотором 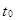 значение
значение 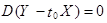 . Следовательно, величина
. Следовательно, величина 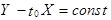 и для некоторого С справедливо равенство
и для некоторого С справедливо равенство 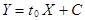 , что требовалось доказать.
, что требовалось доказать.
4. Если X и Y статистически независимы, то 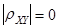 .
.
Свойства 2,4 проверяются непосредственно.
4.5.2. Коррелированность и зависимость системы случайных величин.
Необходимым условием независимости случайных величин X и Y является равенство нулю их корреляционного момента (или коэффициента корреляции). Однако равенство 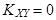 (или
(или 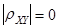 ) есть только необходимое, но недостаточное условие независимости.
) есть только необходимое, но недостаточное условие независимости.
Пример 1.
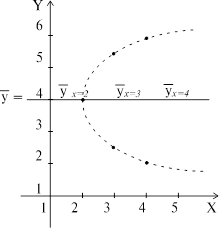
|
На рисунке изображены точки, лежащие на параболе 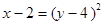 , а
, а 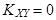 .
.
В связи с этим вводится более узкое понятие некоррелированности (если 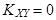 ) или коррелированности (если
) или коррелированности (если 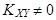 ) случайных величин. Поэтому независимость случайных величин означает и некоррелированность (
) случайных величин. Поэтому независимость случайных величин означает и некоррелированность ( 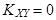 ) и, наоборот, коррелированность (
) и, наоборот, коррелированность ( 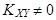 ) – зависимость.
) – зависимость.
В общем случае, когда 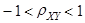 , точки (X,Y) будут разбросаны вокруг прямой тем более тесно, чем больше величина
, точки (X,Y) будут разбросаны вокруг прямой тем более тесно, чем больше величина 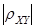 . Таким образом, коэффициент корреляции характеризует не любую зависимость между X и Y, а степень тесноты линейной зависимости между ними.
. Таким образом, коэффициент корреляции характеризует не любую зависимость между X и Y, а степень тесноты линейной зависимости между ними.
Так, в частности, даже при 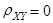 , т.е. при полном отсутствии линейной зависимости, между X и Y может существовать сколь угодно сильная статистическая и даже нелинейная функциональная зависимость (см. пример1).
, т.е. при полном отсутствии линейной зависимости, между X и Y может существовать сколь угодно сильная статистическая и даже нелинейная функциональная зависимость (см. пример1).
При значениях 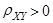 говорят о положительной корреляции между X и Y, означающей, что обе переменные имеют одинаковую тенденцию к возрастанию или убыванию. При
говорят о положительной корреляции между X и Y, означающей, что обе переменные имеют одинаковую тенденцию к возрастанию или убыванию. При 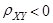 говорят об отрицательной корреляции, означающей противоположную тенденцию в изменении случайных величин X и Y, т.е. одна возрастает, а другая убывает или наоборот.
говорят об отрицательной корреляции, означающей противоположную тенденцию в изменении случайных величин X и Y, т.е. одна возрастает, а другая убывает или наоборот.
Если случайные величины X и Y распределены нормально, то из их некоррелированности следует и их независимость, так как
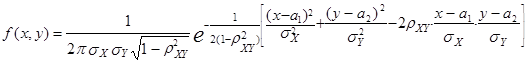 .
.
Если 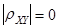 , то
, то 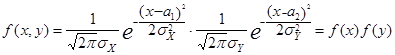 .
.
Для вычисления коэффициента корреляции продолжим пример 2 из §4.1. Воспользуемся формулой
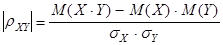 .
.
M(X×Y)=(-200)×(-100)×0,2 + (-200)×0×0,1 + (-200)×(100)×0,05 + 0×(-100)×0,05 + 0×0×0,25 + 0×100×0,02 + 200×(-100)×0,01 + 200×0×0,02 + 200×100×0,3 = 8800$;
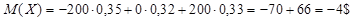 ;
;
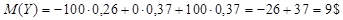 ;
;
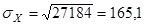 ;
; 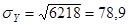 ;
;
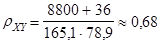 .
.
Пример 2. Закон распределения системы двух случайных величин 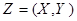 задан таблицей распределения
задан таблицей распределения
| X Y | ||||
| -1 | 0,01 | 0,06 | 0,05 | 0,04 |
| 0,04 | 0,24 | 0,15 | 0,07 | |
| 0,05 | 0,01 | 0,01 | 0,09 |
Найти одномерные (маргинальные) законы распределения X и Y, их математические ожидания, дисперсии и коэффициент корреляции между X и Y.
Решение. Вероятности возможных значений дискретной случайной величины Х, входящей в систему, определяются формулой
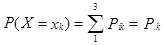 , к=1, 2, 3, 4.
, к=1, 2, 3, 4.
Поэтому одномерное распределение величины Х имеет следующий вид
| X | |||||
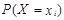
| 0,1 | 0,4 | 0,3 | 0,2 | 1,0 |
Аналогично, пользуясь формулой
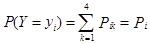 , i=1, 2, 3 ,
, i=1, 2, 3 ,
получим одномерное распределение величины Y
| Y | -1 | |||
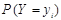
| 0,16 | 0,50 | 0,34 | 1,0 |
Математические ожидания случайных величин X и Y:
M(X)=1,6; M(Y)=0,18.
Дисперсии случайных величин X и Y:
D(X)=0,84; D(Y)=0,47.
Коэффициент корреляции между X и Y вычисляется по формуле
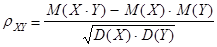 ;
; 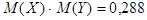 ;
;
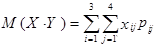 ;
; 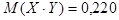 ;
;
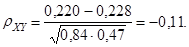
Вопросы для самопроверки.
1. Дайте определение многомерной случайной величины и функции распределения вероятностей.
2. Что называется совместным распределением двумерной дискретной случайной величины (X,Y)? Как оно записывается?
3. Как по известному совместному распределению двумерной случайной величины (X,Y) найти маргинальные распределения составляющих X и Y?
4. Что называется условным распределением составляющей X двумерной дискретной величины (X,Y)?
5. Что называется ковариацией?
6. Что называется коэффициентом корреляции?
7. Укажите свойства коэффициента корреляции.
8. Чему равен коэффициент корреляции случайных величин X и Y = 1 – 2X?
9. В какую величину превращается ковариация двух случайных величин X и Y, если X = Y?
10. Равносильны ли понятия независимости и некоррелированности?
Задачи
4.1. На двух различных рынках города продаются три типа автомобилей (А,В,С). Ниже приведены данные о числе проданных автомобилей за год:
| Рынок | Тип автомобиля | Всего | ||
| А | В | С | ||
| а | ||||
| b | ||||
| Всего |
Найти следующие вероятности: Р(а, А), P(a, B), P(a, C), P(b, A), P(b, B), P(b,С), P(A), P(a/A), P(A/a). Составить таблицу совместных вероятностей.
4.2. Отдыхающие на некотором курорте являются, как правило, бизнесменами (B)или людьми свободных профессий (P)(адвокатами, художниками, врачами и т.д.). Владелец курорта хочет установить, не выгоднее ли ему будет выпускать рекламу двух видов, а не одного. Для этого он поручил своему рекламному отделу подготовить рекламу двух типов – одну для бизнесменов (тип I), другую – для людей свободных профессий (тип II). Реклама была подготовлена, материалы разосланы возможным клиентам, и было получено 800 заявок. Они распределились следующим образом.
| I | II | Всего | |
| Специалисты (P) | |||
| Бизнесмены (В) | |||
| Всего |
а). Найдите вероятности P(B,I); P(B,II); P(I/B).
б). Зависят ли заявки представителей каждой из групп от типа рекламы?
в). Постройте таблицу, согласно данным которой оба типа рекламы отражались бы на заявках одинаково. Найдите соответствующие вероятности P(B,I)и P(B,II).
4.3. Дважды бросается игральная кость. Случайные величины: Х – число появления шестерки, Y – число появлений четной цифры.
а) Описать закон распределения случайного вектора Z = (X,Y).
б) Установить, зависимы или независимы компоненты Х и Y.
в) Описать законы распределения отдельных составляющих.
г) Вычислить вероятность P = {X ³ Y}.
Указание. Для описания закона распределения дискретного случайного вектора (Х,Y)необходимо определить множество всех возможных пар значений  и соответствующие вероятности. Результат представить в виде таблицы.
и соответствующие вероятности. Результат представить в виде таблицы.
4.4. Рассмотрим пространство элементарных событий, состоящее из белых (W), красных (R) и зеленых (G) шаров: 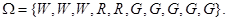 Определим случайную переменную X, равную 0,1 и 2 для W,R,G соответственно. Тогда P(W) = P(X = 0) = 0,3. Выберем теперь два шара (с возвратом) и обозначим результат первого испытания
Определим случайную переменную X, равную 0,1 и 2 для W,R,G соответственно. Тогда P(W) = P(X = 0) = 0,3. Выберем теперь два шара (с возвратом) и обозначим результат первого испытания 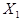 , а второго
, а второго 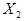 . Вычислить:
. Вычислить:
а) совместное распределение 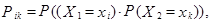 i,k = 1,2,3;
i,k = 1,2,3;
б) одномерные распределения 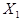 и
и 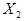 .
.
Являются ли переменные 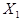 и
и 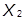 независимыми?
независимыми?
4.5. Рассмотрим задачу 4.4, но будем считать, что после каждого испытания выбранный шар не возвращается. В этом случае
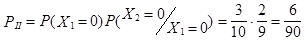 и т.д.:
и т.д.:
Вычислить:
а) совместное распределение 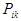 ;
;
б) одномерные распределения 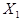 и
и 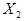 . Являются ли переменные
. Являются ли переменные 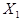 и
и 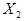 зависимыми? Если ответ положительный, то вычислите коэффициент корреляции.
зависимыми? Если ответ положительный, то вычислите коэффициент корреляции.
Тема 5. Предельные теоремы.
Дата добавления: 2016-06-24; просмотров: 3775;
