Свойства функции распределения многомерной случайной величины.
1. 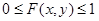 , так как
, так как 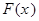 вероятность.
вероятность.
2. 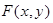 есть неубывающая функция по каждому аргументу, т.е. (см. рис.)
есть неубывающая функция по каждому аргументу, т.е. (см. рис.)

|
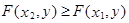 ,если
,если 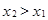 ;
;
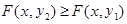 , если
, если 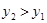 .
.
3. Имеют место предельные соотно- шения:
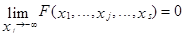
при любых значениях остальных аргументов. Действительно, событие 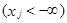 – невозможное, поэтому его совмещение с другими любыми событиями также будет невозможным событием.
– невозможное, поэтому его совмещение с другими любыми событиями также будет невозможным событием.
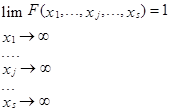

Свойство вытекает из определения, так как события
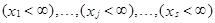 достоверны.
достоверны.
4. а) При 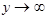 функция распределения системы становится функцией распределения составляющей Х:
функция распределения системы становится функцией распределения составляющей Х:
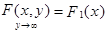 .
.
б) Аналогично, при 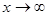 ,
, 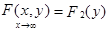 .
.
Плотность распределения вероятностей двумерной случайной величины.
Как и в одномерном случае непрерывную двумерную величину можно задать, пользуясь плотностью распределения, если функция распределения 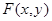 всюду непрерывна и имеет всюду ( за исключением, может быть, конечного числа точек) непрерывную смешанную частную производную второго порядка.
всюду непрерывна и имеет всюду ( за исключением, может быть, конечного числа точек) непрерывную смешанную частную производную второго порядка.
Плотностью распределения 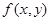 двумерной непрерывной случайной величины
двумерной непрерывной случайной величины  называют вторую смешанную производную от функции распределения, т.е.
называют вторую смешанную производную от функции распределения, т.е.
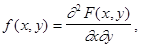
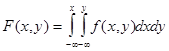 .
.
Свойства плотности распределения:
1. 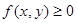 как производная от неубывающей функции
как производная от неубывающей функции 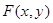 .
.
2. 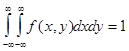 .
.
Дата добавления: 2016-06-24; просмотров: 1028;
