Неравенство Чебышева.

Если известна дисперсия случайной величины, то с ее помощью можно оценить вероятность отклонения этой величины на заданное значение от своего математического ожидания, не зная распределения случайной величины. Эта задача была решена русским математиком П.Л. Чебышевым в 1867 г. Он доказал неравенство для неотрицательной случайной величины X, имеющей

M(X) и D(X):

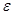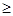P(|X M(X)|< ) 1

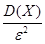
Для доказательства этого неравенства покажем, что выполняется неравенство

P(X ) .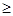

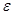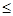
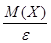Действительно, когда непрерывная случайная величина имеет плотность распределения вероятностей f(x), то

P(X ) = × = = .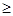

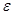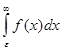
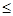
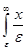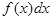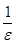
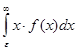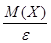Применив это неравенство к неотрицательной случайной величине

M( X M(X)) 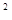, получим, что

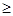
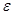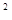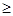
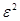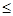
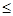
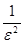P(|X M(X) | ) = P [(( X M(X)) ) ]

M (X M(X)) =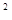

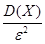
Неравенство Чебышева дает лишь грубые оценки сверху для вероятностей событий вида (|X М (X) | 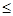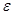). Это “плата” за то, что нам неизвестен закон распределения вероятностей. Так , если оценивать вероятность этого события для нормально распределенной случайной величины X, не зная, что она нормально распределена, то

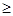P(|X а| 3 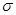) 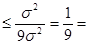0,111...

Ранее (см. правило трех сигм) было найдено точное значение, равное 0,0027. Отсюда видно, что точное значение вероятности в 40 (!) раз меньше ее грубой оценки, полученной на основании неравенства Чебышева.

Пример 1. Сумма всех вкладов в банке составляет 2 млн. долларов., а вероятность того, что случайно взятый вклад не превысит 10000 долл., равна 0,8. Что можно сказать о числе вкладчиков банка?

Решение. Пусть X – сумма случайно взятого вклада, а n – число всех вкладчиков. Тогда

M(X) 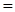2×10 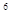/n. Из условия задачи следует, что P( X < 10000) 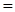0,8. Тогда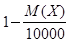 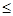0,8. Откуда 200 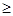n×0,2; n 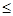1000.

Пример 2. Среднесуточное потребление электроэнергии в населенном пункте равно 20000 квт.ч., а среднее квадратическое отклонение – 200 квт.ч. Какое потребление электроэнергии можно ожидать в этом населенном пункте в ближайшие сутки с вероятностью, не меньшей 0,96?

Решение. По условию задачи M(X) 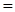20000 квт.ч., 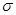(X) 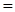200 квт.ч.,

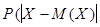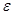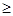< ) 0, 96.

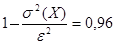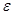
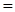
Из неравенства Чебышева известно, что . Определим 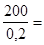1000 квт.ч., 20000-1000 < X < 20000+1000.

Ожидается потребление электроэнергии в пределах от 19000 квт.ч. до
21000 квт.ч.