Центральная предельная теорема.
Изучая нормальный закон распределения, мы отмечали, что в этом случае непрерывная случайная величина формируется под воздействием очень большого числа независимых случайных факторов, причем сила воздействия каждого отдельного фактора мала и не может превалировать среди остальных, а характер воздействия - аддитивный (т.е. при воздействии случайного фактора F на величину 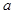 получается величина
получается величина 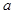 +D(F), где случайная “добавка”, D(F) мала и равновероятна по знаку).
+D(F), где случайная “добавка”, D(F) мала и равновероятна по знаку).
Центральная предельная теорема устанавливает условия образования в пределе нормального закона распределения. Она была открыта Лапласом( опубликована в 1812 г.). Состоит она в следующем.
Рассмотрим сумму S = 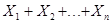 независимых случайных величин. Предположим, что все эти случайные величины имеют одинаковое распределение и принимают целочисленные значения 0; ±1; ±2; ... Распределение
независимых случайных величин. Предположим, что все эти случайные величины имеют одинаковое распределение и принимают целочисленные значения 0; ±1; ±2; ... Распределение 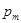 = P(
= P( 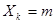 ) каждой из величин
) каждой из величин 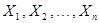 можно изобразить следующим образом.. Нарисуем на каждом m прямоугольник, середина основания которого есть точка m, длина основания равна 1,0 , а площадь есть
можно изобразить следующим образом.. Нарисуем на каждом m прямоугольник, середина основания которого есть точка m, длина основания равна 1,0 , а площадь есть 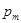 . Получится ряд прямоугольников (с высотами
. Получится ряд прямоугольников (с высотами 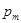 ), сумма площадей которых равна 1
), сумма площадей которых равна 1
(см. рис.1).
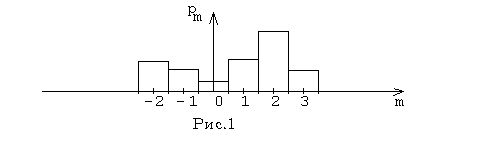
Попытаемся изобразить таким же образом вероятности отдельных значений суммы 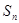 =
= 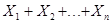 при довольно большом n .
при довольно большом n .
При этом обнаружим, что даже если случайные величины  , i=1,..., n , принимали всего лишь два значения 0 и 1, то значениями суммы
, i=1,..., n , принимали всего лишь два значения 0 и 1, то значениями суммы 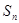 могут быть числа от 0 до n, следовательно, эти значения при большом n просто не поместятся в прежнем масштабе на рис.1, и мы вынуждены будем изменить масштаб, т.е. вместо значений случайной величины
могут быть числа от 0 до n, следовательно, эти значения при большом n просто не поместятся в прежнем масштабе на рис.1, и мы вынуждены будем изменить масштаб, т.е. вместо значений случайной величины
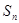 =
= 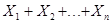
откладывать значения величины
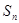 =
= 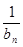 (
( 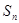 -
- 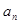 ), где
), где 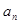 и
и 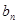 – некоторые числа, зависящие от n .
– некоторые числа, зависящие от n .
Лаплас открыл, что получится нечто замечательное, если положить
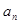 =M(
=M( 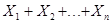 ) = n
) = n 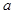 , где
, где 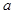 =M(
=M( 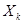 );
);
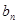 =
= 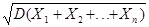 =
= 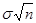 , где
, где 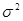 = D(
= D( 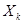 ).
).
Случайную величину
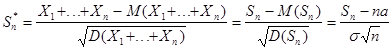
мы будем называть нормированной суммой.
Очевидно, что M( 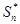 ) = 0, D(
) = 0, D( 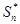 ) = 1, и значениями величины
) = 1, и значениями величины 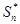 являются числа
являются числа
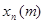 =
= 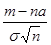 ,
,
причем для любого целого m
P( 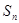 = m) =P(
= m) =P( 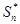 =
= 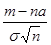 ) = P(
) = P( 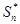 =
= 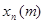 ).
).
Отложим по оси абсцисс значения 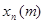 и изобразим вероятности
и изобразим вероятности
P( 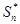 =
= 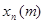 )
)
этих значений прямоугольниками, середины оснований которых лежат в точках 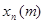 , длины оснований равны расстоянию
, длины оснований равны расстоянию
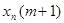 -
- 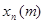 =
= 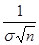
между соседними точками, а площади равны P( 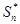 =
= 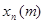 ). Высоты этих прямоугольников равны
). Высоты этих прямоугольников равны
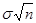 P(
P( 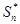 =
= 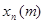 ).
).
При этом произойдет нечто удивительное. Верхние основания этих прямоугольников почти точно лягут на некоторую раз и на всегда вычисленную кривую, задаваемую уравнением
y = 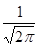
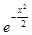 ,
,
которое является плотностью нормального распределения.
При 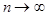 имеем
имеем
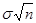 P(
P( 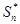 =
= 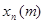 ) ®
) ® 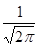
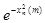 .
.
В таком случае нам известно, что
P( 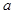
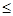
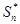
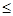
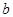 ) » F(
) » F( 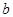 ) – F(
) – F( 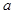 ).
).
Рассмотрим общую часть центральной предельной теоремы в любой ее форме. Пусть 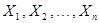 , . . . – последовательность независимых случайных величин с математическим ожиданиями M(
, . . . – последовательность независимых случайных величин с математическим ожиданиями M(  ) и дисперсиями D(
) и дисперсиями D(  ) =
) = 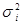 ,
, 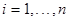 , . . .
, . . .
Введем новые случайные величины:
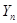 =
= 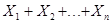 ,
,
для которых
M(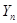 ) =
) = 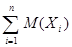 ;
; 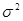 (
(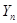 ) =
) = 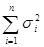 .
.
Тогда при определенных условиях справедливо равенство
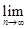 P(½
P(½ 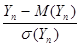 ½< z ) =
½< z ) = 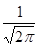
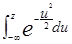 = 0,5 + F(
= 0,5 + F( 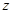 ), утверждающее, что закон распределения нормированных отклонений суммы
), утверждающее, что закон распределения нормированных отклонений суммы 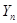 при
при 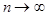 стремится к стандартному нормальному распределению вне зависимостиот типа распределения слагаемых. В таком случае говорят, что
стремится к стандартному нормальному распределению вне зависимостиот типа распределения слагаемых. В таком случае говорят, что 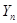 подчиняется асимптотически – нормальному распределению.
подчиняется асимптотически – нормальному распределению.
Различные формы центральной предельной теоремы отличаются друг от друга ограничениями, налагаемыми на последовательность  , при которых выполняется утверждение теоремы. Так, в теореме Муавра-Лапласа в качестве
, при которых выполняется утверждение теоремы. Так, в теореме Муавра-Лапласа в качестве  рассматриваются частоты при i-том испытании в модели Бернулли. Более общим является условие одинакового распределения всех
рассматриваются частоты при i-том испытании в модели Бернулли. Более общим является условие одинакового распределения всех  при существовании конечного математического ожидания M(
при существовании конечного математического ожидания M(  )
) 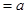 и дисперсии D(
и дисперсии D(  ) =
) = 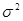 .
.
А.М.Ляпунов, создав специальный метод характеристических функций, используемый в доказательстве различных предельных теорем, показал, что требование одинакового распределения  можно заменить условием их равномерной малости (удельный вес каждого отдельного слагаемого
можно заменить условием их равномерной малости (удельный вес каждого отдельного слагаемого  должен стремиться к нулю при увеличении числа слагаемых). Это условие Ляпунова математически выражается так:
должен стремиться к нулю при увеличении числа слагаемых). Это условие Ляпунова математически выражается так:
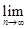
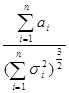 = 0, где
= 0, где 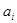 = M½
= M½  – M(
– M(  )½
)½ 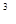 .
.
Практическое использование центральной предельной теоремы.
Оно основано на том, что законы распределения каждой из составляющих сумму величин нам неизвестны и более того, даже перечислить эти величины мы не в состоянии (  ), а поведение суммы оказывается можно предвидеть.
), а поведение суммы оказывается можно предвидеть.
Решение вопроса, при каких значениях n рекомендуется использовать нормальное приближение, зависит от требуемой точности вычисления вероятностей.
Сделаем три замечания о центральной предельной теореме, важные для практики.
Замечание 1. Если предельный вид распределения суммы случайных слагаемых при определенных условиях всегда нормален и не зависит от вида распределения самих слагаемых, то скорость сходимости распределения суммы к нормальному закону существенно зависит от типа распределения исходных компонент. Так, например, при суммировании равномерно распределенных случайных величин уже при 6-10 слагаемых можно добиться достаточной близости к нормальному закону, в то же время как для достижения той же близости при суммировании хи-квадрат распределенных слагаемых понадобится более 100 слагаемых.
Замечание 2. Центральной предельной теоремой не рекомендуется пользоваться для аппроксимации вероятностей на “хвостах” распределения, т.е. при оценке вероятностей больших отклонений анализируемой суммы случайных величин от своего среднего значения. Это приводит к большим относительным ошибкам аппроксимации. Так, например, пусть 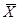 (n) – нормированный среднедушевой доход в семье (соответственно
(n) – нормированный среднедушевой доход в семье (соответственно 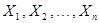 – заработная плата работающих членов семьи и другие составляющие семейного дохода) и пусть нас интересует доля q семей с очень высоким доходом, а именно с доходом, не меньшим некоторого достаточного высокого уровня
– заработная плата работающих членов семьи и другие составляющие семейного дохода) и пусть нас интересует доля q семей с очень высоким доходом, а именно с доходом, не меньшим некоторого достаточного высокого уровня 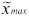 (руб.). Исследования показали, что точное значение этой доли q=0,03, в то время как соответствующая нормальная аппроксимация дала результат
(руб.). Исследования показали, что точное значение этой доли q=0,03, в то время как соответствующая нормальная аппроксимация дала результат 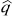 =0,003. Разность
=0,003. Разность 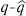 мала (как и следует из центральной предельной теоремы), однако относительная погрешность составляет величину 1000%.
мала (как и следует из центральной предельной теоремы), однако относительная погрешность составляет величину 1000%.
Особенно важным это предостережение оказывается при попытке использования нормальных аппроксимаций в задачах расчета зависимостей типа “пропускная способность” (или предельная прочность) системы – вероятность отказа в обслуживании ( разрушения ).
Замечание 3. Центральная предельная теорема позволяет проследить асимптотические связи, существующие между различными модельными законами распределения, с одной стороны, и нормальным законом – с другой (см. схему ).
Опираясь на центральную предельную теорему, можно объяснить, в частности, следующие полезные для статистической практики выводы:
1. Биномиально распределенная случайная величина X с параметрами n, p асимптотически (по 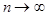 ) нормальна с параметрами M(X) = np и
) нормальна с параметрами M(X) = np и
D(X)= np(1 – p) = npq. Данный результат известен как теорема Муавра – Лапласа (доказана впервые Муавром в 1733 г., когда еще не была известна центральная предельная теорема).
2. Распределение 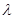 – пуассоновской случайной величины X(
– пуассоновской случайной величины X( 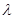 ) асимптотически (по
) асимптотически (по 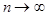 ) нормально с параметрами M(X) = D(X) =
) нормально с параметрами M(X) = D(X) = 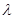 .
.
| Биноминальное распределение |
| Гипергеометрическое распределение |
3. О других распределениях и их связи с нормальным видно на схеме.
| nвелико |
|
Распределение
 Коши Коши
|
| Т-распределение Стьюдента |
Нормальное
  распределение распределение
|
| p<0,1 |
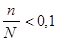
|
|
Распределение
  Пуассона Пуассона
|
 |
| npq>5 |
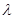 >9 >9
|
| 0,1<n<0,9 |
| n=1 |
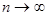
|
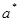
|
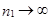
|
 |
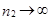
|
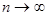
|
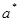
|
Хи – квадрат
 распределение распределение
|
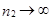
|
 F– распределение F– распределение
|
| Z – распределение |
Схема зависимостей между некоторыми распределениями;
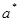 – функциональное преобразование – функциональное преобразование
|
Рассмотрим некоторые примеры практического использования центральной предельной теоремы.
1. Ошибки измерения. Случайная ошибка измерения образуется под воздействием достаточно большого числа факторов, каждый из которых вызывает как бы часть (слагаемое ) суммарной ошибки. Если при этом какой-то фактор оказывает преобладающее воздействие, то и распределение суммарной ошибки будет в основном формироваться его распределением. Однако если все факторы оказываются примерно равноценными, то при достаточно большом их числе можно ожидать почти нормального распределения суммарной ошибки измерения.
2. Рассеивание при стрельбе. Известно, что при стрельбе происходит отклонение от цели точки попадания снаряда. Причиной такого отклонения является суммарное воздействие на снаряд множества факторов, например, ветра, колебания ствола орудия, неоднообразия формы и поверхности снаряда и др. В предположении относительной равноценности воздействия этих факторов и достаточно большого их числа можно ожидать почти нормального распределения суммарного отклонения.
3. Массовое производство. Пусть имеет место устойчивый технологический процесс, с помощью которого производятся некоторые изделия. Будем рассматривать в качестве случайной величины X – отклонение изготовленного изделия от стандарта, на который настроен процесс. Существует огромное количество факторов, оказывающих влияние на процесс ( изменение температуры, качество заготовок и т.д.). Совокупное же их действие дает уже заметный результат: изготовленные изделия имеют различные отклонения от стандарта. Из центральной предельной теоремы следует, что случайная величина X будет иметь распределение, близкое к нормальному.
4. Выборочные наблюдения. Закон больших чисел и центральная предельная теорема являются теоретической основой выборочного метода, широко применяемого в статистике. Суть его состоит в том, что по сравнительно небольшой случайной выборке судят о всей совокупности исследуемых объектов (ее называют генеральной совокупностью). Выборочным аналогом вероятности при большом числе наблюдений является относительная частота. Выборочное среднее арифметическое n одинаково распределенных случайных величин в случае повторной выборки удовлетворяет условиям центральной предельной теоремы и поэтому может рассматриваться как асимптотически нормально распределенная случайная величина.
Пример. На распределительную базу поступило 100 одинаковых ящиков с радиолампами. M(X) числа радиоламп в каждом ящике, которые пришли в негодность за время транспортировки, равно 3, 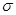 (X) = 2. Определить границы, в которых с вероятностью не менее 0,8, будет заключено общее число радиоламп, пришедших в негодность за время транспортировки.
(X) = 2. Определить границы, в которых с вероятностью не менее 0,8, будет заключено общее число радиоламп, пришедших в негодность за время транспортировки.
Решение. Пусть Y = 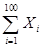 – число радиоламп, пришедших в негодность за время транспортировки. Тогда
– число радиоламп, пришедших в негодность за время транспортировки. Тогда
M(Y) = 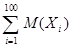 = 100×3 =300, D(Y) =
= 100×3 =300, D(Y) = 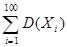 = 400.
= 400.
Воспользуемся теоремой Муавра – Лапласа
P(½ 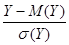 ½<
½< 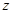 ) = 0,8 ; P( M(Y) –
) = 0,8 ; P( M(Y) – 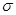 (Y)×
(Y)× 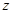 <Y< M(Y)+
<Y< M(Y)+ 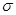 (Y)×
(Y)× 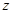 ) = 0,8.
) = 0,8.
По таблице функции Лапласа F( 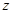 ) = 0,8/2 = 0,4 находим квантиль
) = 0,8/2 = 0,4 находим квантиль
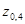 = 1,28. Следовательно, границы, в которых заключено общее число радиоламп, пришедших в негодность, равны (300 ± 26), т.е. (274; 326).
= 1,28. Следовательно, границы, в которых заключено общее число радиоламп, пришедших в негодность, равны (300 ± 26), т.е. (274; 326).
Дата добавления: 2016-06-24; просмотров: 1876;
