I. Математическое ожидание с.в. x.

Лекции по эконометрике

Эконометрика – это наука, объединяющая различные статистические методы, используемые для наблюдения за ходом развития экономики, ее анализа и прогнозов, а также для выявления взаимосвязей между экономическими явлениями.

Задачи:

1) Изучить экономическое явление

2) Прогнозирование явлений

3) Взаимосвязи явлений

Раздел I

Анализ невременных данных

Мы будем работать с данными, которые не являются временными, т.е. их можно переставлять местами, не меняя смысла

Случайная величина (с.в.) x – это числовая функция, заданная на некотором вероятностном пространстве.

Функция распределения с.в. x– это числовая функция числового аргумента, заданная равенством: F(x)=P(x 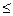C)

Характеристики случайной величины

I. Математическое ожидание с.в. x.

Обозначается E(x). Показывает среднее ожидаемое значение.

Если x – дискретная с.в., то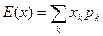

Если x – непрерывная с.в., то 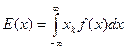, где f(x) – плотность распределения.

Т.к. при работе с данными мы не знаем вероятности, то математическое ожидание считается как 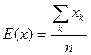, где n – количество наблюдений

Свойства математического ожидания:

1) 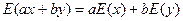, где x и y – с.в.; a и b = const

2)

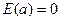
3) Если с.в. y 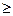с.в. x, то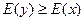

4) Если 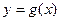, то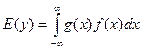

II. Дисперсия

Обозначается D[x]=V(x). Дисперсия – это среднее отклонение от среднего, т.е. на сколько в среднем большинство значений отклонится от математического ожидания, т.е. большинство значений будет лежать в интервале: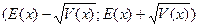

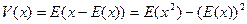
Свойства дисперсии:

1)

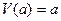
2)

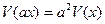
3)

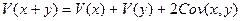
III. Ковариация

Обозначается Cov(x,y). Показывает однонаправленность двух случайных величин, т.е. ковариация – это мера линейной зависимости с.в.

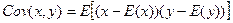
Свойства ковариации:

1)

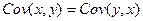
2)

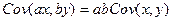
3)

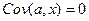
4)

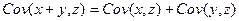
Т.к. ковариация меняется от 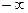до 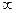, то использовать ее как меру линейной связи, неудобно, поэтому вводят понятие корреляции.

IV. Корреляция.

Обозначается Corr(x,y). Показывает силу линейной связи в интервале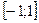

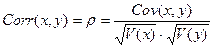
Свойства корреляции:

1)

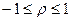
2) Если 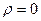, то между x и y связи нет.

3) Если 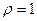, то связь сильная положительная, т.е. рост x вызывает рост y и наоборот.

Замечание: если 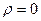, т.е. линейной связи нет, то это не значит, что нет нелинейной связи.

Ложная корреляция.

При использовании 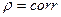следует помнить, что он показывает наличие только линейной связи. Ложная корреляция – в ряде случаев неправильно выбраны случайные величины, между которыми ищется корреляционная связь.

Пример: Если искать связь между длиной волос и ростом, то получится, что чем выше человек, тем короче у него волосы. Ошибка в том, что следует рассматривать эту зависимость отдельно по мужчинам и отдельно по женщинам.

V. Медиана

Медиана – это альтернатива определения среднего значения. Она считается по упорядоченному по возрастанию ряду из наблюдений (вариационный ряд). Показывает среднее из большинства. Обозначается med.

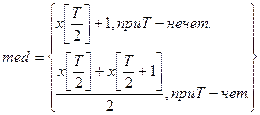
Пример:Имеются 10 человек. 9 человек получают 100$, 1 – 10000$. Найти средний доход человека.

Средний доход человека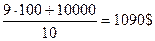

Мы видим, что среднее значение малоэффективно и не показывает реальной ситуации.

Используем медиану.

1)

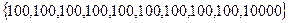
2) т.к. Т=10, то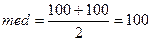

Медиана показала реальное положение вещей.

Медиана используется, когда есть несколько сильных выбросов, т.е. несколько резко выделяющихся от других значений.

VI. Мода.

Мода – это число, делящее выборку пополам, т.е. 50% значений лежит выше нее, а 50% - ниже. Обозначается mod.

Пример: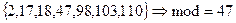

Медиана показывает насколько справедливо среднее.

VII. Оценки

Введем обозначения:

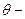истинное значение параметра

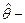оценка параметра

Т.к. истинное значение параметра неизвестно, то мы его находим (оцениваем) по некоторой выборке объема Т.

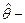то число, которое скорее всего примет истинное значение.

Свойства оценок:

Мы стараемся найти и подобрать выборку таким образом, чтобы по ней получить оценки, которые:

1) состоятельны, т.е. при 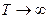оценка стремится к истинному значению, т.е., чем больше выборка, тем точнее оценка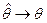

2) несмещенность, т.е. математическое ожидание оценки – это истинное значение, т.е. в среднем мы получаем истинное значение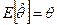

3) эффективность, т.е. дисперсия оценки – минимальна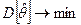

Замечание: дисперсия напрямую связана с точностью оценивания. Чем выше дисперсия, тем больше варьируемость признака, тем менее точный результат мы получаем.