Спецификация модели

Под спецификацией понимают выбор параметров регрессии 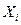. Т.к. на практике исследуется приближенная модель, рассмотрим соотношение между МНК-оценками параметров выбранной и истинной модели.

Рассмотрим два случая:

1) Исключение. В модель не включали существенные параметры. Тогда оценивается модель,

где z - часть существенных параметров.

Мы оцениваем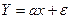

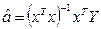
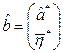- истинная оценка

Найдем математическое ожидание полученной оценки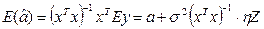

Получаем смещенные оценки, т.е. оценка не такая хорошая, но можно показать, что ее дисперсия будет меньше.

Включение в модель несущественных параметров.

Пусть истинная модель: 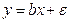, а оценивается модель: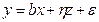

Выписывая оценку коэффициентов b в оцениваемой модели, можно показать, что

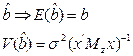
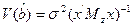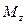оценка несмещенная, но дисперсия , где – матрица, зависящая от z, т.е. дисперсия оценки увеличивается от включения в модель несущественных параметров.

Следствие: выбирая из двух зол наименьшее, лучше не включать часть существенных параметров, чем включить несущественные.