Модель множественной регрессии

Обобщением двумерной или парной линейной регрессии служит многомерная линейная регрессия

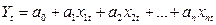-уравнение многомерной линейной регрессии,

где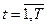

Основные гипотезы:

1)

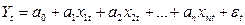
спецификация модели - вид, линейный по параметрам

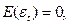
2) 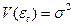- не зависит от t

3) 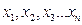- независимые параметры;y– зависимый

4)

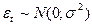
Запишем это уравнение в матричной форме

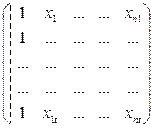
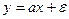
Построить такое уравнение регрессии означает найти оценку параметра, т.е. оценку вектора а.

По теореме Маркова-Гаусса если выполняются основные гипотезы 1,2,3,4, то можно применить метод наименьших квадратов, с помощью которого получится следующее уравнение:

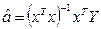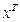, где - икс транспонированный

Т.к. мы находим оценки коэффициентов, а не их истинное значение, то нам хотелось бы оценить точность оценивания.

Она связана с вариацией оценки, т.е. с дисперсией: чем больше дисперсия, тем меньше точность и больше вариация. Тогда:

(**)

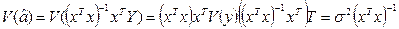Используя правила перемножения матриц, получаем: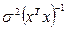

Замечание: из формулы (**) видно, что чем больше параметров, тем больше дисперсия. Поэтому мы выбираем максимально простую модель.

Оценивание качества многомерной линейной регрессии осуществляется так же, как и двумерной, но следует помнить, что 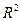растет с увеличением параметров, поэтому с помощью 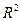можно сравнивать только модели с одинаковым количеством зависимых параметров.