Модель парной линейной регрессии

Пусть Y,X – две выборки объема Т.

Возникает вопрос. Связаны ли они между собой? Если да, то как, и как выразить эту связь количественно?

У

Х

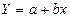
Необходимо подобрать а и bтакими, чтобы линия была как можно ближе ко всем значениям. a иb – неизвестные параметры. Необходимо подобрать a иb, минимизировав меру расстояния от точек, до получившейся прямой. В качестве меры можно взять сумму квадратов отклонения от среднего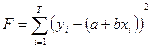

Т.е. мы суммируем квадраты расстояния в каждой точке между наблюдаемым значением и тем, что лежит на линии. Берется квадрат расстояний, чтобы большим расстояниям придать больший вес, а также избежать отрицательных значений.

Иногда в качестве меры отклонения берут модуль расстояния

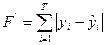
Но вычисления с модулем гораздо сложнее. Мы будем использовать квадрат отклонений.

Для нахождения неизвестных параметров а и b, имея в распоряжении выборки Y и X объема Т, нам необходимо минимизировать следующее расстояние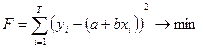

Мы ищем линию, которая будет максимально близко лежать от этих точек.

Применяя метод Лагранжа в решении подобных задач, получаем что:

,

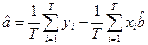где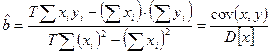

Мы получили оценки неизвестных параметров a и b, удовлетворяющие свойствам оценок, с помощью которых можно построить уравнение регрессии и найти качественную зависимость между X и Y.

, ,

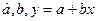
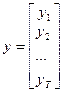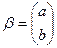- вектор из двух букв a и b.

В данном случае построить регрессию, значит найти оценку вектора .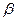

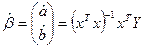- матричная форма записи