Общая методика построения регрессионного уравнения
1) Выбираем зависимую переменную Y.
2) Рассматриваем парные графики зависимостей Y от 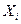
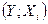 , где
, где 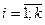 , k – параметр.
, k – параметр.
 |

По виду этого графика делаются выводы о наличии или отсутствии зависимости и о виде этой зависимости.
3) Рассматривается матрица корреляции между зависимой переменной и независимой.
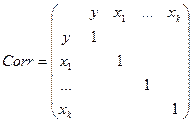
Интерпретируются знаки линейной корреляции и сила линейной связи.
Если 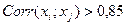 , то один из них исключается
, то один из них исключается
4) С помощью метода пошагового отбора строим регрессию (Y, 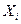 )
)
5) Подбираем спецификацию модели, а именно максимизируя 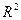 , минимизируется количество параметров линейной регрессии.
, минимизируется количество параметров линейной регрессии.
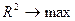 , количество параметров регрессии
, количество параметров регрессии 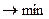
Подбирая спецификацию модели можно использовать следующие соображения:
а) lnY, тогда зависимая переменная не уйдет в минус и зависимость Y от X постепенно, т.е. при изменении параметра X на 1, Y меняется в процентах.
б) берется параметр в квадрате, если с увеличением X его влияние на Y возрастает.
в) ln параметра. В этом случае с ростом значения параметра, влияние на Y уменьшается.
г) использование взаимодействия параметров, например их перемножение.
6) Построение прогноза (точного) наилучшей подобранной модели
7) Построение интервального прогноза, т.е. построение 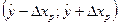
8) (Дополнительно) Работа с выбросами.
После их удаления п.4-п.7 и сравниваются.
9) Интерпретация полученных результатов:
а) описание экономического смысла модели
б) интерпретация коэффициентов и знаков перед ними
в) анализ точности прогнозирования и ширины интервала
г) описание выбросов
Раздел II
Анализ силы связи порядковых и категориальных переменных
Количественные (или номинальные) переменные – переменные, выражающиеся в числах в определенных единицах измерения.
Категориальные переменные – это переменные, принимающие конечное число значений, состоящих из категорий, которые неупорядочены относительно друг друга. Чаще всего выражаются не в числах.
Например: цвет, уровень образования, страна, фамилия.
Порядковые переменные – это категориальные переменные, для которых определено отношение порядка, т.е. они ранжированы относительно друг друга.
Например: оценка успеваемости, номер места на соревнованиях или группы людей по возрастам. В исследовании социально-экономических явлений часто возникает необходимость оценить силу связи между категориальными и порядковыми переменными. Коэффициент корреляции Пирсона, который считали ранее, не подходит, он не показывает реального состояния. Необходимо использовать другие коэффициенты связи.
Пример: Пусть у нас имеется лекарство и мы хотим проверить есть ли связь между приемом этого лекарства и состояния больного.
 x1 x2 x1 x2
| В | 
| Итого по строке |
| А | n11 | n12 | n10 |
| Ā | n21 | n22 | n20 |
| Итого по стобцу | n01 | n02 | N |
Всех больных случайным образом делят на 2 группы. 1-ю группу лечат новым препаратом, а 2-ю группу лечат традиционными методами. Таким образом мы получаем 2 показателя: 1-ый показатель: проходил ли больной курс лечения новым препаратом.
Х1: А – давали лекарство
Ā – не давали
Х2 – результат лечения.
Х2: В – состояние улучшилось
В – состояние ухудшилось
Результаты этого опыта можно представить в таблице.
n11 – число людей, которым давали лекарство и чье состояние улучшилось.
n12 - число людей, которым давали лекарство и чье состояние ухудшилось.
n01=n11+n21
n02=n12+n22
n10=n11+n12
N20=n21+n12
N=n11+n12+n21+n22
Задача состоит в том, чтобы по этим 4-м числам определить, связан ли результат лечения с приемом лекарства и как именно связан.
Рассмотрим разные варианты.
1.Если между Х1 и Х2 нет никакой связи, лекарство бессмысленно. Тогда доля принимавших лекарство среди больных, чье состояние улучшилось должна быть равна доле принимавших лекарство среди тех, кому стало хуже и равна доле принимавших лекарство среди всех больных.
Доля принимающих лекарство, чье состояние улучшилось=n11/n01
Доля принимающих лекарство, чье состояние ухудшилось=n12/n02
Доля принимавших лекарство среди всех участвующих в эксперименте=n11/n01+n12/n02=n10/N
N11=(n11+n12)(n22+n21)/N – то связи нет!
На равенстве долей и построена мера связи. За меру связи можно принять величину n11=…, но у этой величины значения могут быть и больше 1 и меньше 1 по модулюÞ ее необходимо модифицировать, чтобы сделать похожей на коэффициент корреляции. А именно ввести коэффициент Юла, равный D=(n11n22 - n12n21)/(n11n22+n12n21)
Если D=0, то связи нет.
Если связь сильная отрицательная, то коэффициент Юла D=-1
Если связь сильная положительная, то D=1
Замечание: Коэффициент Юла подходит, если рассматривается таблица 2*2. Т.е. определяется сила связи между 2-мя параметрами, каждый из которых принимает только 2 значения.
Связь считается подтвержденной, если ׀D׀>0,5.
Пример 1.
| B | 
| |
| A | n11 | n12 |
| Ā | n22 |
D=(n11n22-0)/(n11n22+0)=1, т.е. из нелечения Þухудшение состояния.
Пример 2.
| n11 | n12 |
| n21 |
D=(0-n12n21)/(0+n12n21)=-1, т.е. из лечения Þухудшение самочувствия или если не лечили, то обязательно стало лучше.
Однако часто в маркетинговых исследованиях приходится сталкиваться с ситуацией, когда 1 или оба признака принимают несколько значений.
В этом случае рассчитать коэффициент Юла не получится и следует использовать другие коэффициенты.
Примером таблиц n*m может служить анализ результатов выборок кандидатов в разных регионах страны. Тогда каждому региону сопоставляют столбец, а каждому кандидату – строку.
В таблице стоят значения рейтинга кандидата в соответствующем регионе. Требуется установить связь между регионом и рейтингом в нем кандидатов. Рассмотрим различия статистики тесноты связи: 1. Фи – коэффициент. Его используют для таблиц 2*2.
Фи= 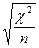 , где
, где
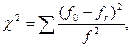
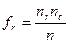
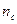 - итоговое число в столбце
- итоговое число в столбце
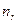 - итоговое число в строке
- итоговое число в строке
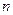 - полный размер выборки
- полный размер выборки
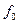 - соответствующее число в таблице
- соответствующее число в таблице
Ф – коэффициент принимающий значение, равное 0, если связь присутствует, и 1, если связь сильная.
Пример. Найти связь между использованием Интернета и полом.
| Исп.интер | М | Ж | Итого |
| Много(>3ч.в день) | |||
| Мало(<3ч.в день) | |||
| Итого |
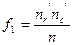 =
= 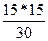 =7,5
=7,5
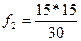 =7,5
=7,5
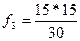 =7,5
=7,5
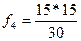 =7,5
=7,5
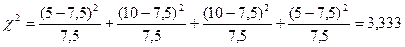
Тогда 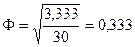
Таким образом связь положительная, не очень сильная.
Ф применяется только для таблиц 2*2, а коэффициент сопряженности С используется в таблице любого размера.
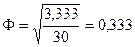
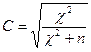
С Î [0;1]
Также используется V – коэффициент Крамера, который является модификацией.
Для таблиц с r рядами
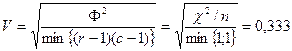 ,
,
т.е. V – коэффициент подтверждает наличие слабой связи.
Дата добавления: 2016-08-07; просмотров: 828;
