Математическим ожиданием числа попаданий

называется среднее число попаданий, которое можно по­лучить, если повторить стрельбу большое число раз в возможно одинаковых условиях.

Математическое ожидание числа попаданий при од­ном выстреле численно равно вероятности попадания.

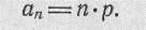
Математическое ожидание числа попаданий при не­скольких выстрелах (а_п), если вероятность попадания (р) для всех выстрелов одинакова, равно произведению количества выстрелов (п) на вероятность попадания при одном выстреле, т. е.

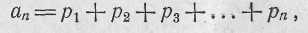
Для случая, когда вероятность попадания от выстре­ла к выстрелу меняется

где 'р1 p2, p3, рп — вероятность попадания при соответст­вующем выстреле.

Пример. Определить математическое ожидание числа попаданий при 5 выстрелах из ручного пулемета Калашникова, если вероят­ность попадания при одном выстреле равна 0,4 и от выстрела к выстрелу не меняется.

Решение. Математическое ожидание числа попаданий равно а_п=п .р=5 . 0,4=2 попаданиям.

Это значит, что при большом числе стрельб по 5 выстрелов на каждую стрельбу будет приходиться в среднем по 2 попадания.

124. Средний ожидаемый расход боеприпасов, необ­ходимых для поражения цели, равен частному от деле­ния требуемого числа попаданий (математического ожи­дания числа попаданий) на вероятность попадания при одном выстреле, т. е.

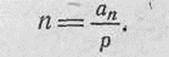
Для стрельбы по живым целям требуемое число по­паданий принимается равным: при стрельбе одиночными выстрелами, когда возможно наблюдение за результата­ми каждого выстрела и стрельба прекращается сразу же

после поражения цели,— одному попаданию;при стрель­бе автоматическим огнем — математическому ожиданию числа попаданий,рассчитанному исходя из заданной ве­роятности поражения цели (надежности стрельбы).

Математическое ожидание числа попаданий в зави­симости от заданной вероятности поражения цели ука­зано в табл. 3 приложения 4.

Пример 1. Определить среднее ожидаемое количество патронов, необходимое для получения одного попадания при стрельбе из са­мозарядного карабина Симонова в наблюдателя противника, если вероятность попадания р = 0,20.

Решение.

Пример 2. Определить среднее ожидаемое количество патронов, необходимое для поражения групповой цели, состоящей из бегущих фигур на фронте 20 м на расстоянии 400 м, при стрельбе из стан­кового пулемета Горюнова с рассеиванием по фронту, если вероят­ность попадания в цель р=0,03 и требуется поразить цель с надеж­ностью Р, =0,50, или 50%.

Решение. 1. Из таблицы 3 приложения 4 находим, что ве­роятности поражения (надежности стрельбы) Pi =0,50 соответствует математическое ожидание числа попаданий а„ = 0,7.

2. Определяем среднее ожидаемое количество патронов, необхо­димое для поражения цели:

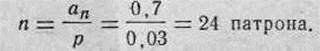
Средний ожидаемый расход патронов (гранат) для поражения цели характеризует экономичность стрельбы, т. е. показывает, каким количеством боеприпасов можно в среднем решить данную огневую задачу.

Средний ожидаемый расход патронов для поражения групповой цели при стрельбе с рассеиванием по фронту можно также определить по формуле

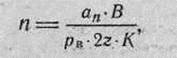
где п — количество патронов, необходимое для пораже­ния заданного числа (процента) фигур; а_п — математическое ожидание числа попаданий, равное: для поражения 80% фигур — 1,609; Для поражения 50% фигур — 0,693 попадания (в при-

ложении 4, таблица 3, эти величины округ­лены);

В — ширина фронта в м, занятого целями; р_а — вероятность попадания в полосу, равную высо­те цели;

2г — ширина отдельной цели; К — коэффициент фигурности цели. 125. Средний ожидаемый расход патронов (п) для поражения цели при стрельбе очередями равен числу выстрелов в очереди (s), деленному на вероятность по­ражения цели при данной длине очереди (Pi),"т. е.

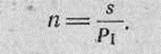
Количество патронов, данное в таблицах стрельбы, рассчитано исходя из характеристики рассеивания для лучших стрелков и длины очереди в 3 патрона.

Пример. Определить среднее количество патронов (л), необхо­димое для поражения пулемета при стрельбе очередями (s) по 3 патрона на расстояние 400 м, если вероятность поражения цели при одной очереди в 3 выстрела Р\ =0,54, или 54%.

Решение. Определим средний ожидаемый расход патронов:

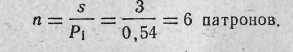
Если известна вероятность попадания в цель (р) и задана надежность стрельбы (Pi), то средний ожидае­мый расход патронов (п) может быть определен по таб­лице 4 приложения 4.

126. Среднее ожидаемое время на выполнение огне­вой задачи складывается из времени на подготовку стрельбы и времени на стрельбу. Время на саму стрель­бу определяется делением среднего ожидаемого расхода боеприпасов на боевую скорострельность оружия с уче­том режима огня.

Среднее ожидаемое время, так же как и средний ожи­даемый расход боеприпасов, характеризует экономич­ность стрельбы.

Наивыгоднейшие значения надежности и экономично­сти стрельбы будут при наибольшей вероятности попа­дания.