Способы определения вероятности попадания

107.Вероятность попадания в цель может быть оп­ределена сравнением площади цели с площадью сердцевины рассеивания, по шкале рассеивания, по таблице значений вероятностей и по сетке рассеивания.

При стрельбе автоматическим огнем (очередями) для вычисления вероятности попадания берутся характери­стики суммарного рассеивания.

108.Если цель по своим размерам равна сердцевине рассеивания или меньше ее, то вероятность попадания в цель определяется приближенно сравнением площади цели с площадью сердцевины рассеивания.При этом до­пускается, что рассеивание пуль впределах сердцевины равномерное.

Вероятность попадания в цель будет во столько раз меньше вероятности попадания в сердцевину, во сколько раз площадь цели меньше площади сердцевины, т. е. р=0,50 х Sa/Св х Сб

где р — вероятность попадания в цель;

0,50, или 50% — вероятность попадания в сердце­вину;

Св и Сб — сердцевинные полосы соответст­венно по высоте и боковому на­правлению; S_n — площадь цели.

Пример. Определить вероятность попадания в грудную фигуру (залегший стрелок) при стрельбе очередями из ручного пулемета Калашникова на 200 м, если средняя траектория пройдет через середину цели.

Решение. 1. Из таблицы находим: Се=0,50 м, Сб=0,50 м; из приложения 4, таблица 6 площадь цели S_n=0,20 м².

2. Определяем вероятность попадания в цель:

Sn 0 20

р = 0,50 • -77Т7- = 0,50 • „ _{РП я ея} = 0,40, или 40%

(0,50 — вероятность попадания в сердцевину).

Пример показывает, что если произвести большое число выстре­лов в возможно одинаковых условиях, то в среднем на каждые 100 выстрелов придется 40 попаданий и 60 промахов, или в среднем на один выстрел приходится 0,40 попадания.

109.Если в каком-либо направлении цель по своим размерам больше сердцевины рассеивания, то вероят­ность попадания в нее может быть определена по шкале рассеивания.При этом вероятность попадания в цель определяется как произведение вероятности попадания в полосу, равную высоте (глубине) цели:

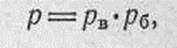
где р — вероятность попадания в цель;

рв — вероятность попадания в полосу, равную высоте цели;

рб — вероятность попадания в полосу, равную шири­не цели.

Для определения вероятности попадания в полосу, равную высоте (ширине) цели, необходимо: вычертить в произвольном масштабе цель и на ней в том же мас­штабе шкалу рассеивания, например, по высоте; подсчи­тать по шкале рассеивания процент попаданий, приходя­щийся в полосу, равную высоте цели; вычертить на цели шкалу рассеивания по боковому направлению и также подсчитать по ней процент попаданий в полосу, равную ширине цели.

При расчетах по шкале рассеивания с масштабом в одно срединное отклонение допускают, что рассеивание равномерно в пределах полосы, равной по ширине одно­му срединному отклонению.

Если цель не является прямоугольником, а имеет фи­гурное очертание, то сначала по шкале рассеивания оп­ределяется вероятность попадания в прямоугольник, описанный вокруг фигурной цели. Затем полученную ве­роятность умножают на коэффициент фигурности, рав­ный отношению площади цели к площади описанного во­круг цели прямоугольника, т. е.

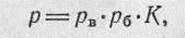
где К — коэффициент фигурности.

При применении коэффициента фигурности допускают, что рассеивание в пределах описанного вокруг цели пря­моугольника равномерно. Это. допущение приводит к ошибке, которая тем больше, чем больше размеры цели по отношению к площади рассеивания. При определении вероятности попадания в фигурную цель коэффициент фигурности можно применять только в тех случаях, ког­да размеры цели меньше размеров полного рассеивания.

Примечание. Для более точных расчетов коэффициент фигурности определяется как отношение вероятности попадания в цель к вероятности попадания в прямоугольник, описанный вокруг цели.

Значения коэффициента фигурности для различных целей даны в приложении 4, таблица 6.

Пример.Определить вероятность попадания в пулемет против­ника при стрельбе из ручного пулемета Дегтярева из положения стоя из окопа на расстояние 300 м, если средняя траектория пройдет через середину цели.

Решение. 1. По таблицам и приложению 4 находим: Вв сум — 0,21 м, Вб сум = 0,29 м, высота цели равна 0,55 м, ширина 0,75 м, коэффициент фигурности К — 0,75.

2. Определяем вероятность попадания в_ полосу, равную высоте цели (рв), для чего:

а) вычерчиваем в произвольном масштабе цель и накладываем на нее (вычерчиваем на ней) в том же масштабе шкалу рассеивания по высоте (Рис. 46);

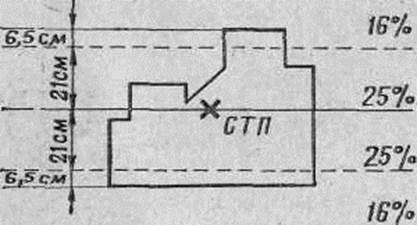
Рис.48. Определение вероятности по­падания по шкале рассеивания в по­лосу, равную высоте цели

б) подсчитываем по шкале рассеивания процент попадания в ту часть шкалы, которой накрывается цель; по одну сторону центра рассеивания цель накрывается полосой, включающей 25% попаданий, и частью полосы, включающей 16% попаданий.

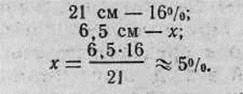
Для определения процента попаданий в эту часть полосы, рав­ную

Следовательно, часть шкалы рассеивания, накрывающая половину цели, включает в себя 6,5 см (27,5—21), составляем пропорцию: Тогда вероятность попадания в полосу, равную высоте цели, будет вдвое больше, т. е.

р_в = 30»/о + 30% = 60°/о, или 0,60.

3. Определяем вероятность попадания в полосу, равную ширине
цели (рб), для чего:

а) накладываем на цель шкалу рассеивания по боковому направлению;

б) подсчитываем по шкале рассеивания процент попаданий, который равен:

Рб = (25»/о + 5°/о) • 2 = 6О»/о, или 0,60.

4. Определяем вероятность попадания в цель:

р = рв-Рб-^С = 0,60-0,60-0,75 = 0,27, или 27»/о.

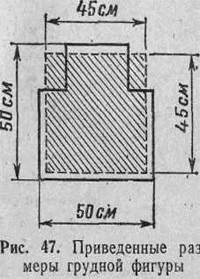
Для удобства определения вероятности попадания иногда фигурную цель заменяют равновеликим прямо­угольником, стороны которого соответственно равны произве­дению ширины (высоты) ми­шени на корень квадратный из коэффициента- * фигурности (Рис. 47).

Приведенные размеры цели даны в приложении 4, табли­ца 6. Найденную вероятность попадания в такой прямоуголь­ник принимают за вероятность попадания в фигурную цель.

ПО. Для более точного оп­ределения вероятности по­падания в цель пользуются таблицей значений вероятно­стей(шкалой рассеивания), рассчитанной с учетом не­равномерности рассеивания через каждую десятую или сотую и т. д. долю срединного отклонения (приложе­ние 4, таблица 1). При этом допускают, что рассеивание равномерно только в пределах полосы по ширине, рав­ной десятой, сотой и т. д. доле срединного отклонения.

Для определения вероятности попадания по таблице значений вероятностей необходимо:

— подсчитать отношения половины высоты (глуби­ны) или ширины цели к срединному отклонению по высоте (дальности) или боковому направлению; эти отно­шения в таблице обозначены через В;

— в графе В найти цифры, соответствующие этим отношениям; стоящие рядом в графе Ф (В) цифры яв­ляются вероятностью попадания в полосы, равные высо­те (глубине) или ширине цели.

Вероятность попадания в цель прямоугольной фор­мы будет равна произведению вероятности попадания в полосу, равную высоте (глубине) цели, на вероятность попадания в полосу, равную ширине цели.

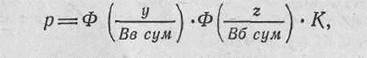
Если цель по своей форме отличается от прямоуголь­ника, то найденную вероятность попадания необходимо умножить на коэффициент фигурности. Вероятность по­падания в такую цель может быть найдена также по приведенным размерам цели без использования коэффи­циента фигурности.

где р — вероятность попадания в цель; у — половина высоты цели; z — половина ширины цели;

Be сум и Вб сум — суммарные срединные отклонения соответственно по высоте и боковому направ­лению; К — коэффициент фигурности.

Пример. Определить вероятность попадания в амбразуру броне­колпака высотой 20 см и шириной 35 см при стрельбе из снайпер­ской винтовки Драгунова на расстояние 400 м, если средняя тра­ектория пройдет через центр цели.

Решение. 1. По таблицам находим: Вв=7,2 см, Вб=7,2 см.

2. Определяем вероятность попадания в полосу, равную высоте цели, для чего:

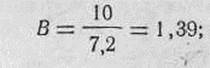
а) находим отношение половины высоты цели к срединному отклонению по высоте:

б) по табл. 1 приложения 4 в графе В находим цифру 1,39; стоящая рядом с этой цифрой в графе Ф (В) цифра 0,652 и есть величина вероятности попадания в данную полосу (р„)-

3. Определяем вероятность попадания в полосу, равную ширине цели:

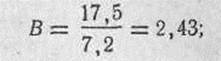
111. Для определения вероятности попадания по таб­лице вероятностей (табл, 2, приложение 4) в круглую мишень при площади рассеивания, близкой по форме к кругу, и при совмещении средней точки попадания с центром мишени необходимо:

— определить отношение радиуса круглой мишени к
радиусу круга рассеивания, вмещающего 50% попаданий;

— по таблице в графе В найти это отношение; стоящая рядом в графе Ф (В) цифра будет являться вероятностью попадания в цель.

Пример. Определить вероятность попадания в круглую мишень (круг) радиусом 10 см при стрельбе из пистолета Макарова на рас­стояние 50 м, если средняя траектория пройдет через центр круга.

Решение; 1. В таблице находим Р5о=8 см.

2. Определяем отношение радиуса круглой мишени (круга) к Р

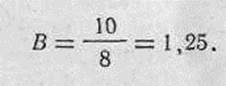
3. По табл. 2 приложения 4 находим в графе В цифру 1,25; рядом стоящая цифра в графе Ф (В) дает вероятность попадания в круг, равную 66,1%.

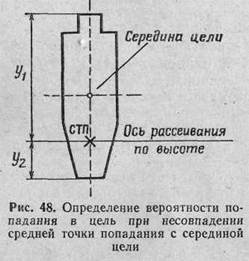
112. Когда средняя точка попадания не совпадает с серединой цели, для определения вероятности попадания в цель необходимо (Рис. 48):

1. Определить вероятность попадания в полосу, рав­ную высоте (глубине) цели, для чего:

а) определить вероятность попадания в полосу, вы­сота (глубина) которой равна расстоянию от оси рассеи­вания по высоте (дальности) до верхнего (дальнего) края цели; для этого найти отношение высоты (глуби­ны) этой полосы к срединному отклонению по высоте (дальности), т. е. В, и по таблице вероятностей взять половину ('/г) значения, указанного в графе Ф (В);

б) определить таким же образом вероятность попа­дания в полосу, высота (глубина) которой равна рас­стоянию от этой же оси рассеивания до нижнего (ближнего) края цели;

в) определить ве­роятность попадания в полосу, равную высоте (глубине) цели; она будет равна: если сред­няя точка попадания расположена в преде­лах цели, — сумме ве­роятностей попадания в эти полосы; если средняя точка попада­ния вне пределов це­ли, — разности вероят­ностей попадания в эти полосы.

2. Подобным же образом определить вероятность попадания в полосу, равную ширине цели.

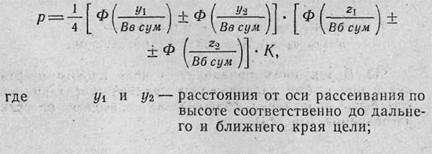
3. Определить вероятность попадания в цель, для его вероятность попадания в полосу, равную высоте цели, умножить на вероятность попадания в полосу, равную ширине цели. Если цель имеет фигурное очертание, то полученную вероятность умножить на коэффициент фигурности или для определения вероятности попадания
взять приведенные размеры цели.

Zi -и z₂ — расстояния от оси рассеивания по боковому направлению соответ­ственно до дальнего и ближнего края цели;

Вв сум и Вб сум— суммарные срединные отклоне­ния соответственно по высоте и боковому направлению; К — коэффициент фигурности.

Знак плюс ( + ) берется, когда ось рассеивания про­ходит через цель, а знак минус (—), когда ось рассеива­ния вне цели.

Пример. Определить вероятность попадания в бегущую фигуру при стрельбе из _пулемета Калашникова на расстояние 500 м, если средняя траектория пройдет ниже середины цели на 0,4 м.:

Решение. 1. По таблицам находим: Be сум—0,37 м, Вб сдм=0,51 м; из приложения 4, таблица 6 находим приведенные раз­меры цели: высота равна 1,40 м, ширина 0,46 м.

2. Определяем вероятность попадания в полосу от оси рассеи­вания по высоте до верхнего края цели:

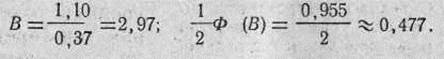
3. Определяем вероятность попадания в полосу от этой же оси рассеивания до нижнего края цели:

4. Определяем вероятность попадания в полосу, равную высоте цели:

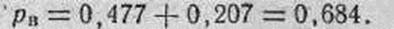
5. Определяем вероятность попадания в полосу, равную ширине
цели, ра:

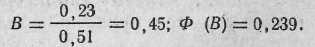
6. Определяем вероятность попадания в цель:

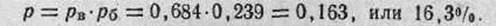
Вероятность попадания в цель любого очерта­ния и при любом расположении средней траектории мо­жет быть определена графическим способом по сетке рассеивания (Рис.49).

Сетка рассеивания оставляется проведением прямых линий, параллельных осям рассеивания, через целые срединные отклонения или доли их. В результате этого вся площадь рассеивания разбивается на ряд прямо­угольников, Вероятности попадания в образовавшиеся

прямоугольники подсчитываются умножением вероятно­стей попадания в полосы, которыми образуются эти пря­моугольники. Например, вероятность попадания в пря­моугольник, отмеченный в табл. 5 приложения 4, рав­на 0,16-0,25 = 0,04, или 4%. Сетка рассеивания в этой таблице дана в масштабе в одно срединное отклонение. Определение вероятности попадания по сетке рассеи­вания производится в той же последовательности, что и по шкале рассеивания. Для этого надо начертить в ус­ловном масштабе цель и на нее наложить в том же мас­штабе сетку рассеивания так, чтобы центр рассеивания был в точке согласно условиям стрельбы. Затем подсчитать вероятность попадания в цель суммированием ве­роятностей попадания в прямоугольники, накрывающие цель; причем там, где прямоугольники не полностью входят в цель, вероятности берутся примерным сравне­нием площади, занятой целью, с площадью всего прямо­угольника.

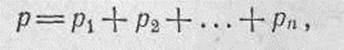
где р— вероятность попадания в цель;

Ри Pi и т. д. — вероятности попадания в прямоуголь­ники.

114. Для определения вероятности попадания в оди­ночную (групповую прерывчатую) цель при стрельбе с искусственным рассеиванием по фронту необходимо най­ти вероятность попадания в полосу, равную высоте цели, и умножить ее на отношение площади одиночной цели (занятой всеми фигурами) к площади прямоугольника, ширина которого равна ширине фронта искусственного рассеивания, а высота — высоте цели. При этом допус­кается, что рассеивание пуль по боковому направлению равномерно и вероятность попадания в полосу, равную фронту цели (рассеивания), равна 100%. Если группо­вая цель состоит из одинаковых по размерам фигур, то ее площадь определяется умножением площади одной фигуры на число фигур.

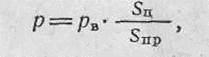
где р — вероятность попадания в цель;

р_в — вероятность попадания в полосу, равную вы­соте цели;

5ц — площадь цели; S_np — площадь прямоугольника.

Пример. Определить вероятность попадания в групповую цель, состоящую из 10 бегущих фигур на фронте 40 м на расстоянии 300 м, при стрельбе из пулемета Калашникова (ПКС) с рассеива­нием по фронту при условии, что ось рассеивания по высоте пройдет через середину цели.

Решение. I. По таблицам находим: Вв=0,15 м; при стрельбе с рассеиванием по фронту Be увеличивается в 1,4 раза; из прило­жения 4, таблица 6 высота цели равна 1,5 м, площадь одной фигуры цели 0,64 м².

2. Определяем срединное отклонение по высоте при стрельбе с рассеиванием по фронту:

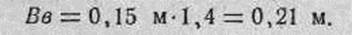
3. Определяем вероятность попадания в полосу, равную высоте цели:

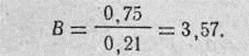
По табл. 1 приложения 4 находим:

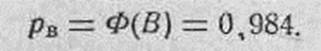
4. Определяем вероятность попадания в групповую цель:

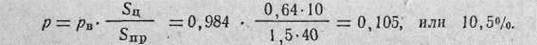
115. Вероятность попадания в цель с учетом ошибок в подготовке стрельбы определяется вышеуказанными способами. При этом, кроме характеристик рассеивания, учитываются ошибки в подготовке стрельбы (см. ст. 103 и 104) и принимается, что средняя точка попадания про­ходит через середину цели.

Пример. Определить вероятность попадания в появляющееся реактивное противотанковое ружье при стрельбе из пулемета Ка­лашникова на расстояние 600 м с учетом возможных ошибок в стрельбе; ветер боковой; расстояние до цели определено глазомерно.

Решение. 1. По таблицам находим: Вв сум—0,44 м, Вб ct/jn = 0,61 м; из приложения 4, таблицы 7 и 6 £в=0,63 м, Ен = 0,43 м, приведенные размеры цели: высота равна 0,85 м, ширина 0,85 м.

2. Определяем суммарные (приведенные) ошибки в подготовке стрельбы:

а) по высоте:

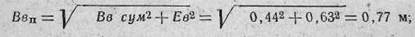
б) по боковому направлению:

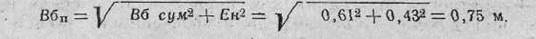
3. Определяем вероятность попадания в цель: а) в полосу, равную приведенной высоте цели:

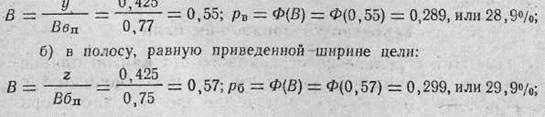
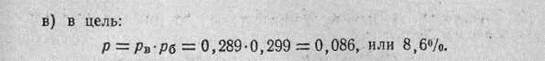
116. Вероятность попадания при стрельбе из автома­та, а также из ручного пулемета из положения с колена, стоя, на ходу с короткой остановки определяется выше­указанными способами отдельно для первых пуль оче­редей и для последующих пуль очередей.

Пример. Определить вероятность попадания в грудную "фигуру при стрельбе из автомата Калашникова (АКМ) из положения лежа с упора на расстояние 400 м при условии, что ошибок в стрельбе нет.

Решение. 1. По таблицам находим: Bei — 0,17 м, £<?i=0,I5 (для первых пуль очередей); Вв_ПОс=0,23 м, Вб_Пос = 0,36 м (для последующих луль очередей); из приложения 4, таблица 6 приве­денные размеры грудной фигуры: высота=0,45 м, ширина = 0,45 м.

2. Определяем вероятность попадания для первой пули очереди:

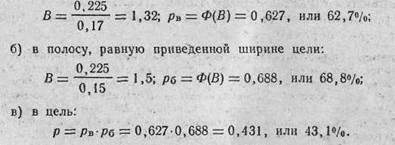
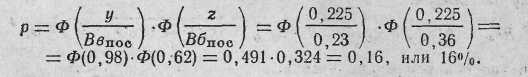
а) в полосу, равную приведенной высоте цели:

Вероятности попадания для первой пули очереди идля последующей пули очереди и коэффициент зависи­мости между ними затем учитываются при определении вероятности поражения цели заданным количеством патронов.

3. Определяем вероятность попадания для любой последующей пули

Вероятность пораженияцели

117.Пристрельбе из стрелкового оружия по одиноч­ным живым целям ииз гранатометов по одиночным бро­нированным целям однопопадание обычно дает поражение цели. Поэтому под вероятностью поражения оди­ночной цели понимается вероятность получения хотя бы одного попадания при заданном числе выстрелов.

118. Вероятность поражения цели при одном выстре­ле (Pi) численно равняется вероятности попадания в цель (/?). Расчет вероятности поражения цели при этом условии сводится к определению вероятности попадания в цель.

Пример. Определить вероятность поражения снайпера против­ника (грудная фигура) с первого выстрела из Снайперской винтовки обр. 1891/30 г. на расстояние 500 м; расстояние до цели определено глазомерно.

Решение. 1. По таблицам находим: Вв=0,08 м; £6=0,08 м; из приложения 4, таблицы 7 и 6 ошибка в подготовке стрельбы по высоте £е=0,36 м, приведенные размеры цели: высота равна 0,45 м, ширина 0,45 м.

2. Определяем суммарную (приведенную) ошибку в подготовке стрельбы по высоте:

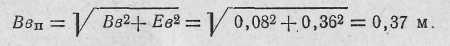
3. Определяем вероятность попадания в цель: а) в полосу, равную приведенной высоте цели:

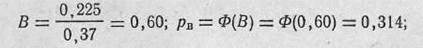
б) в полосу, равную приведенной ширине цели:

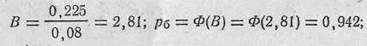
в) в цель:

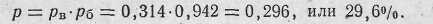
Так как при попадании пули в снайпера будет наверняка полу­чено его поражение, найденное значение вероятности попадания . и есть вероятность поражения цели с первого выстрела, т. е. /?=/>! =29,6%.

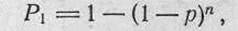
119. Вероятность поражения цели (Pi) при несколь­ких одиночных выстрелах, одной очередью или несколь­кими очередями-, когда где (1—р)—вероятность промаха вероятность попадания для всех выстрелов одинакова, равна единице минус вероятность промаха в степени, равной количеству выстрелов (я), т.е.

Пример.Определить вероятность поражения реактивного про­тивотанкового ружья при стрельбе из пулемета Калашникова одной очередью в 5 выстрелов на расстояние 600 м; ветер боковой; рас­стояние до цели определено глазомерно.

Решение. 1. По таблицам находим: Вв сум=0,44 м, Вб сум—0,61 м; из приложения 4, таблицы 7 и 6 срединная ошибка по высоте £s=0,63 м, по боковому направлению £к=0,43 м, коэф­фициент фигурности 0,72.

2. Определяем суммарную (приведенную) ошибку в подготовке стрельбы по. высоте:

Bs_n = Y ^{Be с}У^м2 + ^Ев2 = У 0,442 + 0,632 = 0,77 м.

3. Определяем суммарную (приведенную) ошибку в подготовке стрельбы по боковому направлению:

Вб_п = У Вб сум? + £«2 ₌ у о,612+,0,432 ₌ о,7бм,

4. Определяем вероятность попадания в цель;

\ Вбп ) \ 0,77 / \0,75У '

= Ф(0,65).ф(0,67)-0,72 =0,339-0,349-0,72 = 0,085, или 8,5»/о.

5. Определяем вероятность поражения цели очередью в 5 выст­релов:

Р, = 1 — (1 — pyi = 1 — (1 — 0,085)5 = 0,36, или 8,5%.

Найденная таким образом вероятность поражения це­ли характеризует надежность стрельбы, т. е. показывает, в скольких случаях из ста в среднем цель в данных ус­ловиях будет поражена не менее чем при одном попада­нии. По условиям примера при большом числе подобных стрельб в среднем на каждые 100 стрельб в 36 стрельбах будет получено не менее одного попадания в цель, в 64 стрельбах цель не будет поражена.

Стрельба считается достаточно надежной, если веро­ятность поражения цели не менее 80%.

120.Вероятность поражения цели при нескольких вы­стрелах одной очередью или несколькими очередями, когда вероятность попадания первых и последующих пуль (очередей) изменяется от выстрела (очереди) к вы­стрелу (очереди), равна единице минус вероятность про­махов первых и последующих пуль очереди (очередей):

а) для одной очереди:

Р₁ = 1 — (1 _ р_пер). (1 _ р_иоау-1 •

б) для нескольких очередей (вероятность попадания от очереди к очереди не изменяется):

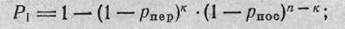
в) когда осуществляется ввод корректур (вероят­ность попадания от очереди к очереди изменяется):

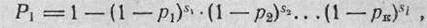
где п — общее количество выстрелов;

к — количество очередей; Su Sz, Si — количество выстрелов в очереди; Ри рг, Рк — вероятность попадания при одном вы­стреле первой, второй и т. д. очереди.

Пример. Определить вероятность поражения пулемета из автома­та Калашникова (АК.М) одной очередью в 3 выстрела при стрель­бе стоя из окопа на расстояние 300 м; ошибок в подготовке стрель­бы нет (средняя траектория пройдет через середину цели).

• Решение. 1. По таблицам находим: Sei=0,12 м, 5<5i = 0,ll м,
Вв сг//Ипос = 0,23 м, Вб сум_ааа=0,33 м; из приложения 4, таблица б
приведенные размеры цели равны: высота равна 0,48 м, ширина
0,65 м. . ... ..

2. Определяем вероятность попадания для первой пули оче­реди:

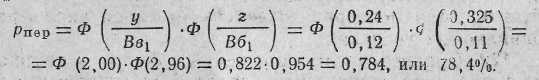
3. Определяем вероятность попадания для последующей пули очереди:

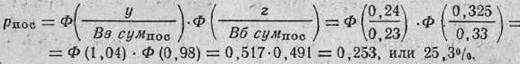
4. Определяем вероятность поражения цели очередью в 3 вы­стрела:

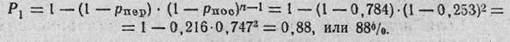
Если вероятность попадания от выстрела к выстрелу не изменяется, вероятность поражения цели может быть определена по таблице вероятностей поражения цели (приложение 4, таблица 4), рассчитанной для различной величины вероятности попадания {/?) и числа выстре­лов (л).

Пример.Определить вероятность поражения противотанкового гранатомета при стрельбе из ручного пулемета Калашникова одной очередью в 5 выстрелов, если вероятность попадания равна 0,30.

Решение. По таблице 4, приложение 4 в вертикальной графе, обозначенной буквой р, находим значение вероятности попадания, равное 0,30; в горизонтальной строчке против числа, соответствую­щего числу выстрелов (п), равному 5, находим вероятность пора­жения цели; она равна Pj =0,83, или 83%.

При определении вероятности поражения целей авто­матическим огнем по формулам, указанным в ст. 11.9 и 120, получаются завышенные результаты (на 3—7%). Поэтому при более точных подсчетах вероятностей пора­жения цели пользуются специальными формулами, учи­тывающими коэффициент зависимости выстрелов.