Лекция 2. Математическое моделирование сложных систем
Основные обозначения и определения
Концептуальная (содержательная) модель – абстрактная модель, определяющая состав и структуру системы, свойства ее элементов и причинно-следственные связи, присущие исследуемой системе, существенные для достижения цели моделирования. Пример описания концептуальной модели см. на рис. 2.1
| Генераторы рабочей нагрузки |
| Генераторы возмущающих воздействий |
| Управляющие воздействия |
| Продукты преобразования |
| Информация о состояниях |
Рисунок 2.1 – Пример графического описания концептуальной модели
Система S – совокупность элементов со связями и целью функционирования F.
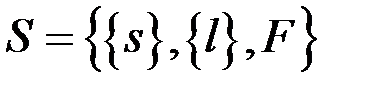
Элементs есть некоторый объект, обладающий определенными свойствами, внутреннее строение которого для целей исследования не играет роли.
Связь Lмежду элементами есть процесс их взаимодействия, важный для целей исследования.
Цель функционированияесть задача получения желаемого состояния системы. Достижение цели обычно влечет целенаправленное вмешательство в процесс функционирования системы, которое называется управлением.
Параметры системы - это характеристики 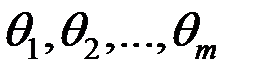 системы, остающиеся постоянными на всем интервале T.
системы, остающиеся постоянными на всем интервале T.
Переменныебывают зависимые и независимые.
Независимые переменные – это, как правило, входные воздействия (в том числе управляющие) ими могут быть также воздействия внешней среды.
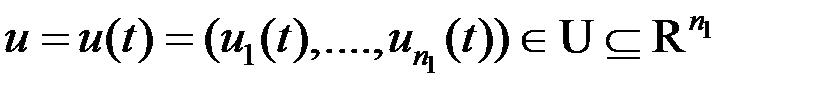
Зависимые переменные – выходные характеристики (сигналы).
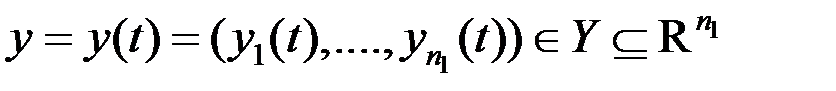
Множество переменных вместе с законами функционирования называется математической моделью системы. Общая схема математической модели представлена на рис. 2.2.
I zUvOT8nMS7dVCg1x07VQUiguScxLSczJz0u1VapMLVayt+PlAgAAAP//AwBQSwMEFAAGAAgAAAAh ADxeeHPBAAAA2gAAAA8AAABkcnMvZG93bnJldi54bWxEj8FqwzAQRO+F/oPYQm+N3BAH40Y2TiBN rk3S+2JtZVNr5UpK4vx9VCj0OMzMG2ZVT3YQF/Khd6zgdZaBIG6d7tkoOB23LwWIEJE1Do5JwY0C 1NXjwwpL7a78QZdDNCJBOJSooItxLKUMbUcWw8yNxMn7ct5iTNIbqT1eE9wOcp5lS2mx57TQ4Uib jtrvw9kqKKJfGpNx/k7z9aJZ7D7z5mdQ6vlpat5ARJrif/ivvdcKcvi9km6ArO4AAAD//wMAUEsB Ai0AFAAGAAgAAAAhAASrOV4AAQAA5gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVz XS54bWxQSwECLQAUAAYACAAAACEACMMYpNQAAACTAQAACwAAAAAAAAAAAAAAAAAxAQAAX3JlbHMv LnJlbHNQSwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEgAAAAAAAAAAAAAAAAAuAgAAZHJzL3Bp Y3R1cmV4bWwueG1sUEsBAi0AFAAGAAgAAAAhADxeeHPBAAAA2gAAAA8AAAAAAAAAAAAAAAAAnwIA AGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPcAAACNAwAAAAA= "> I zUvOT8nMS7dVCg1x07VQUiguScxLSczJz0u1VapMLVayt+PlAgAAAP//AwBQSwMEFAAGAAgAAAAh AG03DTXAAAAA2gAAAA8AAABkcnMvZG93bnJldi54bWxEj0GLwjAUhO+C/yE8wZumirhSjSLKwoKC tBa8PppnW2xeShO1/nsjCHscZuYbZrXpTC0e1LrKsoLJOAJBnFtdcaEgO/+OFiCcR9ZYWyYFL3Kw Wfd7K4y1fXJCj9QXIkDYxaig9L6JpXR5SQbd2DbEwbva1qAPsi2kbvEZ4KaW0yiaS4MVh4USG9qV lN/Su1FwSvCA++lstthn2U9yvOzSm06VGg667RKEp87/h7/tP61gDp8r4QbI9RsAAP//AwBQSwEC LQAUAAYACAAAACEABKs5XgABAADmAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNd LnhtbFBLAQItABQABgAIAAAAIQAIwxik1AAAAJMBAAALAAAAAAAAAAAAAAAAADEBAABfcmVscy8u cmVsc1BLAQItABQABgAIAAAAIQAzLwWeQQAAADkAAAASAAAAAAAAAAAAAAAAAC4CAABkcnMvcGlj dHVyZXhtbC54bWxQSwECLQAUAAYACAAAACEAbTcNNcAAAADaAAAADwAAAAAAAAAAAAAAAACfAgAA ZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA9wAAAIwDAAAAAA== ">
Рисунок 2.2 – Общая схема математической модели системы
Непрерывно–детерминированные модели (D – схемы) (рис. 2.3). Непрерывные детерминированные модели используют дифференциальные уравнения. Данные схемы отражают динамику процессов, протекающих во времени в системе. В общем виде модель описывается следующим образом:

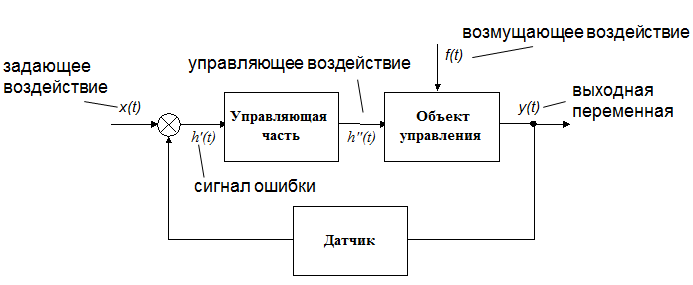
Рисунок 2.3 – Графическое представление схемы отражения динамики процессов, протекающих во времени
Далее будут рассмотрены примеры моделей.
Модель Мальтуса – описывает динамику изменения некоторой популяции:
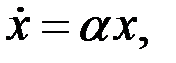
где 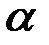 — некоторый параметр, определяемый разностью между рождаемостью и смертностью. Иными словами, Скорость роста пропорциональна текущему размеру популяции. Решением этого уравнения является экспоненциальная функция
— некоторый параметр, определяемый разностью между рождаемостью и смертностью. Иными словами, Скорость роста пропорциональна текущему размеру популяции. Решением этого уравнения является экспоненциальная функция 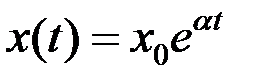 . Если рождаемость превосходит смертность (
. Если рождаемость превосходит смертность ( 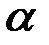 >0), размер популяции неограниченно и очень быстро возрастает. Понятно, что в действительности этого не может происходить из-за ограниченности ресурсов. При достижении некоторого критического объёма популяции модель перестает быть адекватной, поскольку не учитывает ограниченность ресурсов. Уточнением модели Мальтуса может служить логистическая модель, которая описывается дифференциальным уравнением Ферхюльста
>0), размер популяции неограниченно и очень быстро возрастает. Понятно, что в действительности этого не может происходить из-за ограниченности ресурсов. При достижении некоторого критического объёма популяции модель перестает быть адекватной, поскольку не учитывает ограниченность ресурсов. Уточнением модели Мальтуса может служить логистическая модель, которая описывается дифференциальным уравнением Ферхюльста
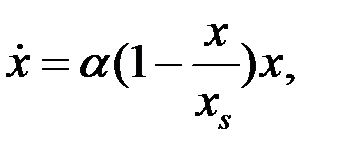
где  — «равновесный» размер популяции, при котором рождаемость в точности компенсируется смертностью. Размер популяции в такой модели стремится к равновесному значению
— «равновесный» размер популяции, при котором рождаемость в точности компенсируется смертностью. Размер популяции в такой модели стремится к равновесному значению  , причем такое поведение структурно устойчиво.
, причем такое поведение структурно устойчиво.
Модель Ло́тки — Вольтерра. Модель взаимодействия двух видов типа "хищник - жертва", названная в честь её авторов (Лотка, 1925; Вольтерра 1926), которые предложили модельные уравнения независимо друг от друга. Такие уравнения можно использовать для моделирования систем «хищник-жертва», «паразит-хозяин», конкуренции и других видов взаимодействия между двумя видами (Одум, 1986). В математической форме предложенная система имеет следующий вид:
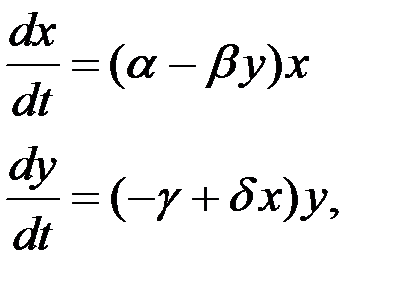
где 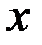 — количество жертв,
— количество жертв, 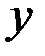 — количество хищников,
— количество хищников, 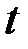 — время,
— время, 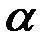 ,
, 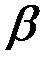 ,
, 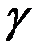 и
и 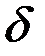 — коэффициенты, отражающие взаимодействия между видами.
— коэффициенты, отражающие взаимодействия между видами.
Модели в пространстве состояний. Пространство состояний — в теории управления один из основных методов описания поведения динамической системы. Движение системы в пространстве состояний отражает изменение ее состояний. В пространстве состояний создаётся модель динамической системы, включающая набор переменных входа, выхода и состояния, связанных между собой дифференциальными уравнениями первого порядка, которые записываются в матричной форме. В отличие от описания в виде передаточной функции и других методов частотной области, пространство состояний позволяет работать не только с линейными системами и нулевыми начальными условиями. В пространстве состояний относительно просто работать с MIMO-системами. Схема модели в пространстве состояний изображена на рис. 2.4.
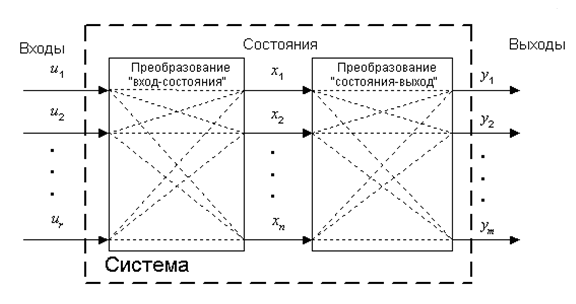
Рисунок 2.4 – Схема модели в пространстве состояний
Для случая линейной системы с 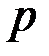 входами,
входами, 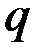 выходами и
выходами и 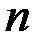 переменными состояния описание имеет вид:
переменными состояния описание имеет вид:
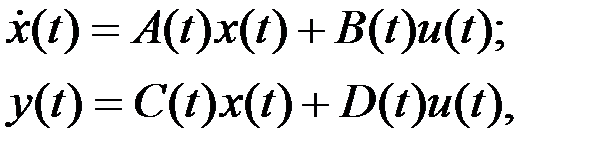
где 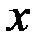 – вектор состояния,
– вектор состояния, 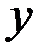 — вектор выхода,
— вектор выхода, 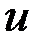 — вектор управления,
— вектор управления, 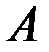 матрица системы,
матрица системы,  — матрица управления,
— матрица управления, 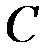 — матрица выхода,
— матрица выхода, 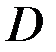 — матрица прямой связи.
— матрица прямой связи.
Дискретно–детерминированные модели ( F – схемы ). Основным видом дискретно- детерминированных моделей является конечный автомат. Конечным автоматом называют дискретный преобразователь информации, способный под воздействием входных сигналов переходить из одного состояния в другое и формировать сигналы на выходе. Это автомат с памятью. Для организации памяти в описание автомата вводят автоматное время и понятие состояние автомата.
Понятие «состояние» автомата означает, что выходной сигнал автомата зависит не только от входных сигналов в данный момент времени, но и учитывает входные сигналы, поступающие ранее. Это позволяет устранить время как явную переменную и выразить выходные сигналы как функцию состояний и входных сигналов.
Всякий переход автомата из одного состояния в другое возможен не ранее, чем через дискретный интервал времени. Причем сам переход считается, происходит мгновенно, то есть не учитывают переходные процессы в реальных схемах.
Существует два способа введения автоматного времени по которому автоматы делятся на синхронные и асинхронные.
В синхронных автоматах моменты времени, в которых фиксируются изменения состояний автомата, задаются специальным устройством - генератором синхросигналов. Причем сигналы поступают через равные интервалы времени - 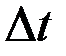 . Частота тактового генератора выбирается такой, чтобы любой элемент автомата успел закончить свою работу до появления очередного импульса.
. Частота тактового генератора выбирается такой, чтобы любой элемент автомата успел закончить свою работу до появления очередного импульса.
В асинхронном автомате моменты перехода автомата из одного состояния в другое заранее не определены и зависят от конкретных событий. В таких автоматах интервал дискретности является переменным.
Также существуют детерминированные и вероятностные автоматы.
В детерминированных автоматах поведение и структура автомата в каждый момент времени однозначно определены текущей входной информацией и состоянием автомата.
В вероятностных автоматах они зависят от случайного выбора.
Абстрактно конечный автомат можно представить как математическую схему (F–схему), которая характеризуется шестью видами переменных и функций:
- конечное множество x(t) входных сигналов (входной алфавит);
- конечное множество y(t) выходных сигналов (выходной алфавит);
- конечное множество z(t) внутренних состояний (алфавит состояний);
- начальное состояние автомата z0, 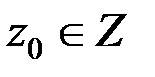 ;
;
- 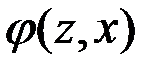 – функция переходов автомата из одного состояния в другое;
– функция переходов автомата из одного состояния в другое;
- 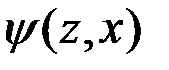 – функция выходов автомата.
– функция выходов автомата.
Абстрактный конечный автомат имеет один вход и один выход. В каждый дискретный момент времени t=0,1,2,... F-автомат находится в определенном состоянии z(t) из множества Z - состояний автомата, причем в начальный момент времени t=0 он всегда находится в начальном состоянии z(0)=z0. В момент t , будучи в состоянии z(t), автомат способен воспринять на входном канале сигнал 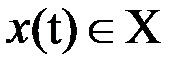 и выдать на выходном канале сигнал
и выдать на выходном канале сигнал 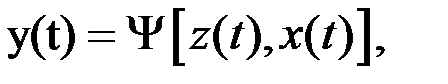 переходя в состояние
переходя в состояние 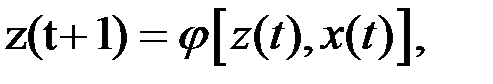 где
где 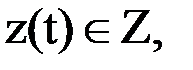
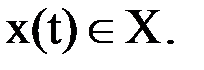
Абстрактный конечный автомат реализует некоторое отображение множества слов входного алфавита X на множество слов выходного алфавита Y, то есть, если на вход конечного автомата, установленного в начальное состояние 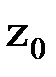 , подавать в некоторой последовательности буквы входного алфавита
, подавать в некоторой последовательности буквы входного алфавита 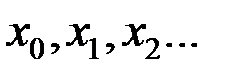 , которые составляют входное слово, то на выходе автомата будут последовательно появляться буквы выходного алфавита
, которые составляют входное слово, то на выходе автомата будут последовательно появляться буквы выходного алфавита  , образуя выходное слово.
, образуя выходное слово.
Следовательно, работа конечного автомата происходит по следующей схеме: на каждом t-ом такте на вход автомата, находящегося в состоянии 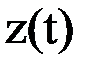 , подается некоторый сигнал
, подается некоторый сигнал 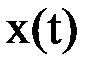 , на который автомат реагирует переходом на
, на который автомат реагирует переходом на 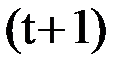 -ом такте в новое состояние
-ом такте в новое состояние 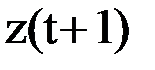 и выдачей некоторого выходного сигнала.
и выдачей некоторого выходного сигнала.
В зависимости от способа определения выходного сигнала абстрактные конечные автоматы (синхронные) подразделяются на два типа:
- 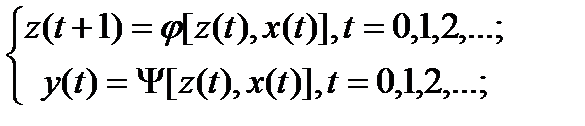 F – автомат первого рода, автомат Мили:
F – автомат первого рода, автомат Мили:
- F – автомат второго рода,автомат Мура:
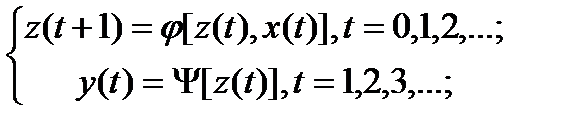
 Чтобы задать конечный F – автомат, необходимо описать все элементы множества
Чтобы задать конечный F – автомат, необходимо описать все элементы множества
Пример конечного автомата (рис. 2.5).
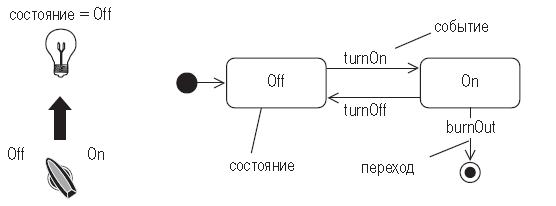
Рисунок 2.5 – Пример конечного автомата
- состояние (state) –ситуация, при которой автомат осуществляет некоторую деятельность или ожидает некоторого события;
- событие (event) – происшествие, занимающее определенное положение во времени и пространстве;
- переход (transition) – переход из одного состояния в другое в ответ на событие.
Дискретно – стохастические модели ( Р - схемы). Дискретно-стохастические модели называют также вероятностными автоматами. В общем, виде вероятностный автомат является дискретным потактным преобразователем информации с памятью, функционирование которого в каждом такте зависит только от состояния памяти в нем и может быть описано статистически.
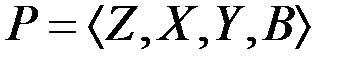 Частным случаем Р– автомата, задаваемого
Частным случаем Р– автомата, задаваемого
являются автоматы, у которых либо переход в новое состояние, либо выходной сигнал определяются детерминировано (Z– детерминированный вероятностный автомат, Y– детерминированный вероятностный автомат соответственно).
Схемы вероятностных автоматов (Р-схем) применяются:
- в проектировании дискретных систем, проявляющих статистически закономерное случайное поведение;
- в определении алгоритмических возможностей систем;
- в обосновании границ целесообразности их использования;
- в решении задач синтеза по выбранному критерию дискретных стохастических систем, удовлетворяющих заданным ограничениям.
Математическое понятие Р-автомата формируется на понятиях, введенных для F'-автомата.
Пример Р-схемы.
 Y–детерминированный Р–автомат задан таблицей переходов и таблицей выходов:
Y–детерминированный Р–автомат задан таблицей переходов и таблицей выходов:
| Z | z0 | z1 | z2 | z3 | z4 |
| Y |

Требуется оценить суммарные финальные вероятности пребывания этого автомата в состоянии z2 и z3.
Дискретно – непрерывные модели. В комбинированных дискретно-непрерывных моделях независимые переменные могут изменяться как дискретно, так и непрерывно. В рамках методологии комбинированного моделирования исследуемая система описывается с помощью элементов, их атрибутов и переменных состояния. Поведение системы имитируется путем вычисления значений переменных состояния через небольшие отрезки времени и значений атрибутов элементов в моменты свершения событий.
Процессы в линейных импульсных и цифровых системах описываются дискретно – разностными уравнениями вида:
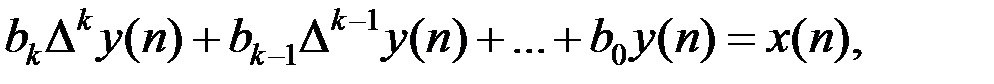
где x(n) – решетчатая функция входного сигнала;
y(n) – решетчатая функция выходного сигнала, которая определяется решением данного уравнения; bk – постоянные коэффициенты; ∆k y(n) – разность к – го порядка; n – номер отсчета.
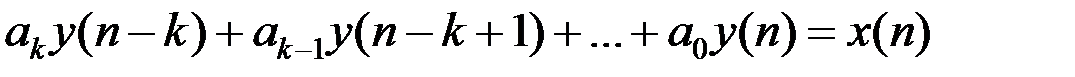
Основным математическим аппаратом моделирования цифровых систем является Z– преобразование.
Дата добавления: 2016-06-24; просмотров: 2151;
