Непрерывно–стохастические модели (Q– схемы).

Q–схемы применяются при формализации процессов функционирования систем, которые по своей сути являются процессами обслуживания.

При непрерывно-стохастическом подходе в качестве типовых математических схем применяется система массового обслуживания (англ. queueing system) (см. рис. 2.6), которые будем называть Q-схемами. Системы массового обслуживания представляют собой класс математических схем, разработанных в теории массового обслуживания и различных приложениях для формализации процессов функционирования систем, которые по своей сути являются процессами обслуживания.

В качестве процесса обслуживания могут быть представлены различные по своей физической природе процессы функционирования экономических, производственных, технических и других систем.

При этом характерным для работы таких объектов является случайное появление заявок (требований) на обслуживание и завершение обслуживания в случайные моменты времени, т. е. стохастический характер процесса их функционирования.

В любом элементарном акте обслуживания можно выделить две основные составляющие:

- ожидание обслуживания заявки;

- собственно обслуживание заявки.

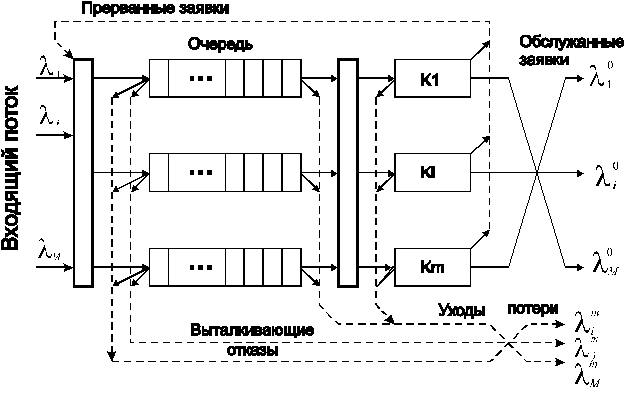
Рисунок 2.6 – Модель СМО

Основные операции математического моделирования:

1. Линеаризация.

2. Идентификация.

3. Оценка адекватности (точности) модели.

4. Оценка устойчивости модели.

5. Оценка чувствительности модели.

6. Организация вычислительного эксперимента для моделирования.

Линеаризация – процесс замены нелинейных зависимостей математической модели линейными или кусочно-линейными зависимостями с целью упрощения процесса моделирования.

Методы линеаризации:
1) Метод логарифмирования – применяется к степенным функциям;
2) Метод обратного преобразования – для дробных функций;
3) Комплексный метод – для дробных и степенных функций.

Идентификация – процесс поиска значений параметров (структуры) мат. модели.

Цель идентификации – построение надежной, адекватной, эффективно функционирующей, гибкой модели на основе минимального объема информативной последовательности сообщений.

Наиболее часто используемыми на практике методами идентификации систем являются:

- метод наименьших квадратов;

- метод максимального правдоподобия;

- метод байесовских оценок;

- метод марковских цепных оценок;

- метод эвристик;

- экспертное оценивание и др.

Адекватностью называется совпадение модели c исследуемой системой в отношении цели моделирования.

Процедура оценки адекватности основана на сравнении измерений на реальной системе и результатов экспериментов на модели (см. рис. 2.7) и может проводиться различными способами. Наиболее распространенные из них:

- по средним значениям откликов модели и системы;

- по дисперсиям отклонений откликов модели от среднего значения откликов системы;

- по максимальному значению относительных отклонений откликов модели от откликов системы.

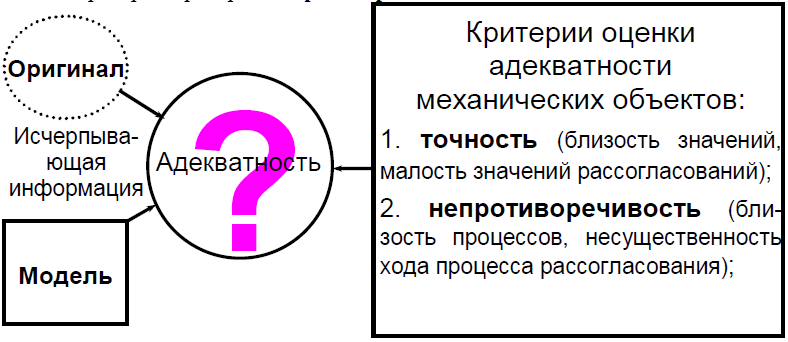
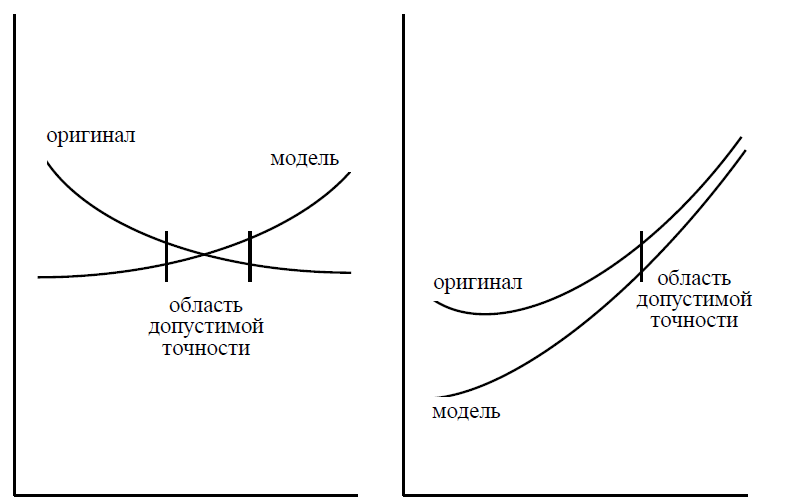
Рисунок 2.7-2.8 – Оценка адекватности модели

Для проверки адекватности необходимо иметь:

- исчерпывающую информацию о реальном случае (что всегда трудно, а подчас бывает практически невозможно);

- результаты контрольного вычислительного эксперимента, воспроизводящего известный реальный случай;

- критерий оценки точности математической модели;

- критерий проверки непротиворечивости математической модели.

Устойчивость модели – это ее способность сохранять адекватность при исследовании эффективности системы на всем возможном диапазоне рабочей нагрузки, а также при внесении изменений в конфигурацию системы. Универсальной процедуры проверки устойчивости модели не существует. Для проверки гипотезы об устойчивости результатов может быть использован критерий Уилкоксона, который служит для проверки того, относятся ли две выборки к одной и той же генеральной совокупности (т. е. обладают ли они одним и тем же статистическим признаком). Критерий предназначен для сопоставления показателей, измеренных в двух разных условиях на одной и той же выборке испытуемых. Он позволяет установить не только направленность изменений, но и их выраженность, то есть способен определить, является ли сдвиг показателей в одном направлении более интенсивным, чем в другом.

Оценку чувствительности модели проводят по каждому параметру 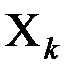в отдельности. Основана она на том, что обычно диапазон возможных изменений параметра известен. Алгоритм оценивания:

1. Вычисляется величина относительного среднего приращения параметра .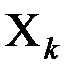

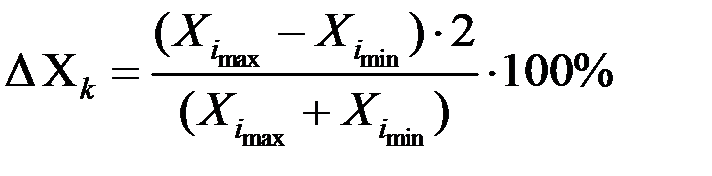
(2.1)

2. проводится пара модельных экспериментов при значениях 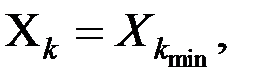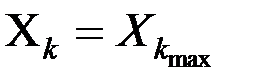и средних фиксированных значениях остальных параметров. Определяются значения отклика модели 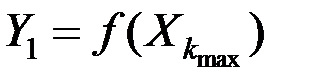и .

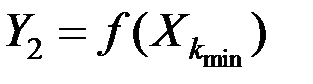3. Вычисляются относительное приращение наблюдаемой переменной .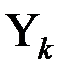

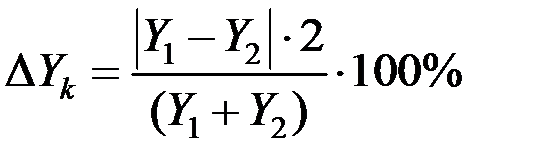(2.2)

Лекция 3. Планирование вычислительных экспериментов

Важнейшей составной частью научных исследований является эксперимент, основой которого является научно поставленный опыт с точно учитываемыми и управляемыми условиями. Основной целью эксперимента является выявление свойств исследуемых объектов, проверка справедливости гипотез и на этой основе широкое и глубокое изучение темы научного исследования.