Введение в теорию моделирования

Моделирование (в широком смысле) – это основной метод исследования во всех областях знаний. Методы моделирования используются для оценок характеристик сложных систем и принятия научно обоснованных решений в разных сферах человеческой деятельности. Существующую или проектируемую систему можно эффективно исследовать с помощью математических моделей (аналитических и имитационных) с целью оптимизации процесса функционирования системы. Модель системы реализуется на современных компьютерах, которые в этом случае выступают в качестве инструмента экспериментатора с моделью системы.

В настоящее время моделирование широко используется в сфере управления различными системами, где основными являются процессы принятия решений на основе получаемой информации. Методы моделирования находят применение при исследовании, проектировании, внедрении вычислительных систем (ВС) и автоматизированных систем управления (АСУ).

Основные определения:

Моделирование –процесс замещения исследуемого объекта или процесса его условным образом или другим объектом (моделью) и исследование свойств оригинала на основании анализа свойств модели.

Модель (от латинского modus - копия, образ, очертание) – объект произвольной природы, который отражает важные, с точки зрения решаемой задачи, свойства объекта исследования (оригинала).

Цель и условия целесообразности создания моделей

Цель моделирования:получение информации о поведении или свойствах реального объекта (процесса)

Условия целесообразности создания моделей:

- Модель устраняет проблемы, связанные с изучением свойств реального объекта.

- Модель обеспечивает адекватное (корректное) отображение исследуемых свойств оригинала.

Формальная классификация моделей

Формальная классификация моделей часто строится в форме дихотомий:

- линейные или нелинейные;

- сосредоточенные или распределённые;

- детерминированные или стохастические;

- статические или динамические;

- абстрактные или материальные;

- дискретные или непрерывные.

- и так далее.

Классификация подходов к моделированию приведена на рис. 1.1.

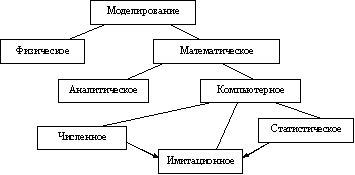
Рисунок 1.1 – Классификация подходов к моделированию

Основные условия выбора подхода обусловлены следующими факторами:

- постановкой задачи;

- составом, характером и объемом исходных данных;

- сложностью объекта моделирования;

- временем на решение исследовательской задачи.

Физическое (натурное) моделирование.При физическом (натурном) моделировании исследуемая система заменяется соответствующей ей другой материальной системой, которая воспроизводит свойства изучаемой системы с сохранением их физической природы. Примером этого вида моделирования может служить пилотная сеть, с помощью которой изучается принципиальная возможность построения сети на основе тех или иных компьютеров, коммуникационных устройств, операционных систем и приложений.

Характеристики:

- Измерение характеристик осуществляется на исследуемых системах в реальном времени (проведение экспериментов).

- Данные исследователь получает, ведя наблюдение за процессами в реальной системе.

Достоинства

- Высокая адекватность модели реальной системе.

- Высокая точность результатов.

Недостатки

- Высокая стоимость создания модели.

- Большие временные затраты.

- Необходимость доработки отдельных узлов реальной системы для проведения натурных экспериментов.

При оптимизации сетей во многих случаях предпочтительным оказывается использование математического моделирования. Математическая модель представляет собой совокупность соотношений (формул, уравнений, неравенств, логических условий), определяющих процесс изменения состояния системы в зависимости от ее параметров, входных сигналов, начальных условий и времени. Иными словами, математическая модель– это формализованное описание системы на некотором абстрактном языке, например, в виде математических формул или алгоритма.

Ниже представлена математическая модель цифрового фильтра (рис. 1.2):

Рисунок 1.2 – Модель цифрового фильтра

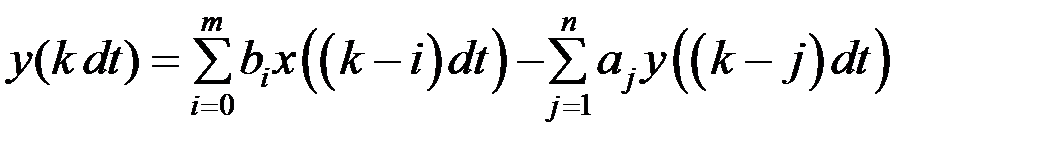
Математические модели бывают следующих типов:

- Структурные модели. Представляют объект как систему со своим устройством и механизмом функционирования.

- Функциональные модели. Отражают только внешне воспринимаемое поведение объекта. В их предельном выражении они называются также моделями «чёрного ящика»

- Возможны также комбинированные типы моделей, которые иногда называют моделями «серого ящика».

Иерархия математических моделей:

- Микроуровень – используются распределенные модели (представляются дифференциальными уравнениями в частных производных). В основном такие модели используются для проектирования сложных физических и химических процессов.

- Макроуровень – сосредоточенные модели (линейные и нелинейные дифференциальные уравнения). В таких моделях принято допущение о дискретизации пространства и времени и выделяется одна независимая переменная – время.

- Функционально-логический уровень – здесь абстрагируются от элементов системы и рассматривают систему с помощью аппарата передаточных функций (для аналоговых систем) и аппарата математической логики и конечных автоматов (для дискретных случаев).

- Системный уровень– используется для анализа очень сложных объектов (общество, тел. сети, предприятия и т.д.). Применяют теорию массового обслуживания, сети Петри и т.д.

Аналитическое математическое моделирование. Для аналитического моделирования характерно, что процессы функционирования системы записываются в виде некоторых функциональных соотношений (алгебраических, дифференциальных, интегральных уравнений). Аналитические модели применяются для относительно простых систем, для исследования характеристик которых не требуется высокая точность.

Достоинства

- Простота и низкая стоимость модели.

- Возможность быстро получить численные результаты.

Недостатки

- Большое число допущений и ограничений.

- Не высокая точность результатов .

- Большая сложность аналитического описания. функциональных зависимостей.

Имитационное моделирование – совокупность методов алгоритмизации, функционирования объектов, описания случайных внешних и внутренних факторов. Суть имитационного моделирования (ИМ) заключается в имитации процесса функционирования системы во времени, с соблюдением таких же соотношений длительности операций как в системе оригинале. При этом имитируются элементарные явления, составляющие процесс, сохраняется их логическая структура, последовательность протекания во времени. В результате применения ИМ получают оценки выходных характеристик системы, которые необходимы при решении задач анализа, управления и проектирования.

Выполняется всегда на ЭВМ в виде вычислительных экспериментов.

Достоинства

- Возможность описания поведения элементов системы на высоком уровне детализации.

- Возможность исследования динамики взаимодействия компонент системы во времени.

- Отсутствие ограничений между параметрами имитационной модели и состоянием внешней среды.

Недостатки

- Меньшая универсальность результатов.

- Необходимость специализированных средств моделирования.

Классификация имитационных моделей

По способу представления в модели динамики систем:

- На основании событий. Событие – это мгновенное изменение некоторого элемента системы или системы в целом.

- На основании анализа работы элементов системы. Работа – это единичное действие по обработке входящих данных.

- На основании анализа процессов. Процесс – это логически связанный набор работ.

- На основании анализа транзакций.

По способу изменения модельного времени:

- Модели с постоянным шагом.

- Модели, работающие по прерываниям.

Все этапы процесса моделирования определяются поставленной задачей и целями моделирования. В общем случае процесс построения и исследования модели можно представить схемой на рис. 1.3.

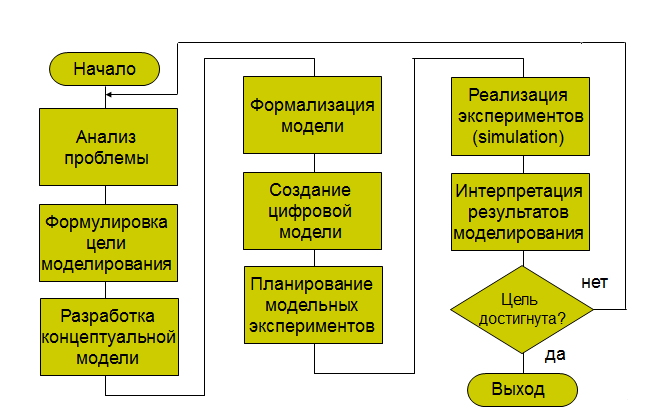
Рисунок 1.3 – Алгоритм процесса моделирования

Структура имитационного моделирования представлена на рис. 1.4.

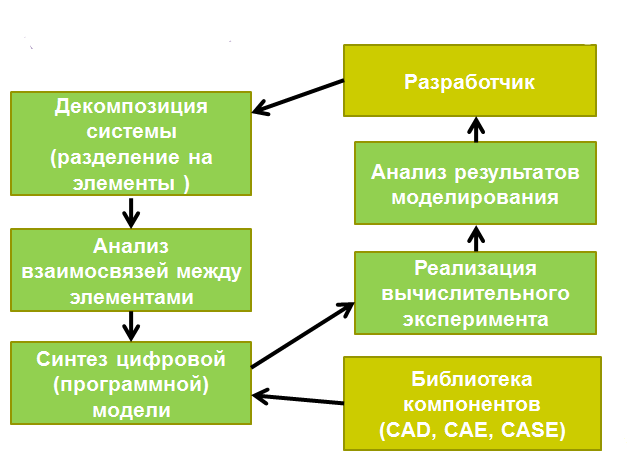
Рисунок 1.4 – Структура имитационного моделирования

Основные принципы моделирования

1. Принцип информационной достаточности. Информации об исследуемом объекте должно быть достаточно для создания модели.

2. Принцип осуществимости. Создаваемая модель должна обеспечивать достижение поставленной цели моделирования с определенной вероятностью и за определенный конечный промежуток времени (P(t0)>P0).

3. Принцип множественности модели. Модель должна отражать исследуемые свойства некоторого семейства объектов.

4. Принцип агрегирования. Подразумевается возможность декомпозиция модели на элементы и создание моделей отдельных элементов.

5. Принцип параметризации (упрощения модели). Модели некоторых элементов (связей) могут быть заменены одним или несколькими параметрами.