Выборочные и теоретические величины. Несмещенность, эффективность и состоятельность статистической оценки параметров. Элементы теории корреляции.
До сих пор мы предполагали, что имеется точная информация о рассматриваемой случайной переменной (т.е. об ее распределении вероятностей (в случае дискретной переменной) или о функции плотности распределения (в случае непрерывной переменной)). Используя эту информацию можно рассчитать теоретическое математическое ожидание 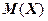 , дисперсию
, дисперсию  и любые другие характеристики.
и любые другие характеристики.
Однако на практике мы не знаем точного вероятностного распределения или плотности распределения вероятностей, а лишь знаем результаты выборочного наблюдения. Понятия «генеральная совокупность», «выборка», «репрезентативность выборки» и способы отбора изложены в первой главе, здесь необходимо отметить, что результаты выборочных значений 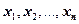 количественного признака
количественного признака  для лучшей обозримости, облегчения обработки этих статистических данных упорядочивают ( по возрастанию, по совпадающим значениям, по интервалам и т.п.).
для лучшей обозримости, облегчения обработки этих статистических данных упорядочивают ( по возрастанию, по совпадающим значениям, по интервалам и т.п.).
Обычно упорядочивают по неубыванию: 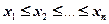 . Разность между максимальным и минимальным значениями СВ
. Разность между максимальным и минимальным значениями СВ  называется размахом выборки (размахом варьирования).
называется размахом выборки (размахом варьирования).
Пусть выборка состоит из 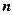 элементов (наблюдении), причем
элементов (наблюдении), причем 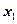 наблюдалось
наблюдалось 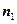 раз,
раз, 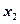 -
- 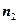 раз, … ,
раз, … , 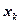 -
- 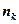 раз и
раз и 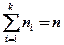 - объем выборки. Наблюдаемые значения
- объем выборки. Наблюдаемые значения 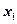 называют вариантами, а последовательность вариант, записанных в возрастающем порядке, - вариационным рядом. Числа наблюдений
называют вариантами, а последовательность вариант, записанных в возрастающем порядке, - вариационным рядом. Числа наблюдений 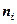 называют частотами, а отношения
называют частотами, а отношения 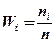 - относительными частотами.
- относительными частотами.
Перечень вариант и соответствующих им частот (или относительных частот) в виде таблицы называют статистическим распределением выборки. Статистическое распределение можно задать также в виде последовательности интервалов и соответствующим их частот ( в качестве частоты, соответствующей определенному интервалу, принимают сумму частот элементов 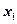 , попавших в этот интервал).
, попавших в этот интервал).
Заметим, что в теории вероятностей под распределением понимают соответствие между возможными значениями СВ и их вероятностями, а в математической статистике – соответствие между наблюдаемыми вариантами и их частотами (или относительными частотами).
Оценкой теоретической функции распределения 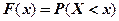 является эмпирическая функция распределения (функция распределения выборки) – которая определяется как относительная частота события
является эмпирическая функция распределения (функция распределения выборки) – которая определяется как относительная частота события 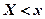 :
: 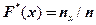 , где
, где 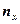 - число значений СВ
- число значений СВ  , меньших, чем
, меньших, чем 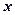 ,
, 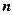 - объем выборки.
- объем выборки.
Например, чтобы найти 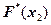 , надо число вариант, меньших
, надо число вариант, меньших 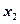 , разделить на объем выборки:
, разделить на объем выборки:  . Из теоремы Бернулли следует, что относительная частота события
. Из теоремы Бернулли следует, что относительная частота события 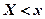 , т.е.
, т.е.  стремится по вероятности к вероятности
стремится по вероятности к вероятности 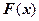 этого события. Другими словами, при больших
этого события. Другими словами, при больших 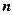 числа
числа  и
и 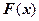 мало отличаются одно от другого. Следовательно, целесообразно использовать эмпирическую функцию распределения выборки для приближенного представления теоретической (интегральной) функции распределения генеральной совокупности.
мало отличаются одно от другого. Следовательно, целесообразно использовать эмпирическую функцию распределения выборки для приближенного представления теоретической (интегральной) функции распределения генеральной совокупности.
Такое заключение подтверждается и тем, что  обладает всеми свойствами
обладает всеми свойствами 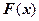 .
.
Пример 2.8.Анализируется прибыль 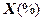 предприятий отрасли. Обследованы
предприятий отрасли. Обследованы  предприятий, данные по которым занесены в статистический ряд:
предприятий, данные по которым занесены в статистический ряд:

| |||||
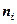
| |||||
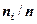
| 0,05 | 0,2 | 0,4 | 0,25 | 0,1 |
Необходимо построить эмпирическую функцию распределения  и ее график (рис.2.8)
и ее график (рис.2.8)
|
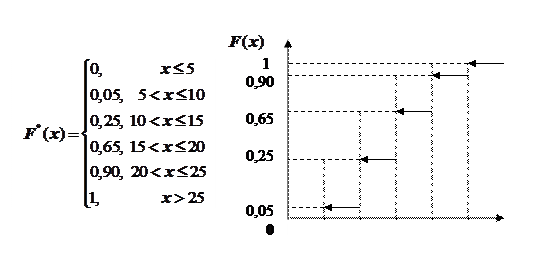
Рис. 2.8
Наглядно статистический ряд может быть представлен в виде полигона частот (или относительных частот) – это ломанная, отрезки которой соединяют точки 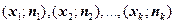 . Для построения полигона частот на оси абсцисс откладывают варианты
. Для построения полигона частот на оси абсцисс откладывают варианты 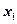 , а на оси ординат – соответствующие им частоты
, а на оси ординат – соответствующие им частоты 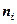 . Соединив точки
. Соединив точки 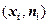 получают полигон частот. Аналогично получают полигон относительных частот.
получают полигон частот. Аналогично получают полигон относительных частот.
При большом объеме выборки ее элементы удобно сгруппировать в интервальный статистический ряд. Для этого вес интервал со всеми 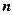 наблюдаемыми значениями выборки разбивают по
наблюдаемыми значениями выборки разбивают по 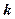 интервалам равной длины
интервалам равной длины 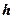 (
( 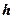 - шаг разбиения). Число
- шаг разбиения). Число 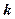 выбирает исследователь исходя из целесообразного количества групп. Интервальный статистический ряд наглядно представляется в виде гистограммы – гистограммой частот называют ступенчатую фигуру из прямоугольников, основаниями которых служат частичные интервалы длиною
выбирает исследователь исходя из целесообразного количества групп. Интервальный статистический ряд наглядно представляется в виде гистограммы – гистограммой частот называют ступенчатую фигуру из прямоугольников, основаниями которых служат частичные интервалы длиною 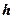 , а высоты равны отношению
, а высоты равны отношению 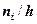 (плотность частоты). Площадь i – го частичного прямоугольника равна
(плотность частоты). Площадь i – го частичного прямоугольника равна 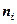 - сумме частот вариант i – го интервала. Следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки
- сумме частот вариант i – го интервала. Следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки 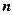 .
.
Аналогично определяется гистограмма относительных частот.
На основании гистограммы обычно выдвигают предположение о виде закона распределения исследуемой величины, что позволяет придать определенную направленность исследованиям.
Пример 2.9Для анализа доходов населения исследованы 300 семей. По уровню дохода население подразделено на 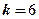 групп. Полученные данные сгруппированы в следующий интервальный статистический ряд:
групп. Полученные данные сгруппированы в следующий интервальный статистический ряд:
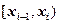
| 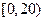
| 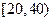
| 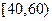
| 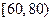
| 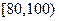
| 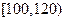
|
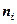
| ||||||
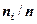
| 1/30 | 5/30 | 8/30 | 10/30 | 4/30 | 2/30 |
Необходимо построить гистограмму и выдвинуть предположение о виде закона распределения СВ  - дохода населения.
- дохода населения.
В последнюю группу могут быт включены все субъекты, чей доход превышает 100. Для получения теоретических выводов последний интервал полагается той же длины ( 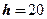 ), что и остальные.
), что и остальные.
Построим гистограмму:
|

Рис. 2.9
Форма гистограммы соответствует нормальному закону распределения, т.е. предполагаем, что СВ  имеет нормальное распределение:
имеет нормальное распределение:  ~
~ 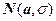 . Далее следует определить параметры
. Далее следует определить параметры 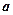 (мат. ожидание) и
(мат. ожидание) и  (среднее квадратическое отклонение).
(среднее квадратическое отклонение).
Пусть объем генеральной совокупности равен N. Тогда математическим ожиданием СВ  является генеральное среднее, а дисперсией - генеральная дисперсия:
является генеральное среднее, а дисперсией - генеральная дисперсия:
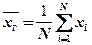 ,
, 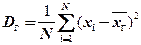 . (2.71)
. (2.71)
Корень квадратный из генеральной дисперсии называется генеральным средним квадратическим отклонением. Таким образом, для нахождения генеральных числовых характеристик необходим анализ всей совокупности. Это требует больших затрат времени и материальных средств, а если объем генеральной совокупности и вовсе неизвестен, то задача не решаема. В реальности же задача решается (хотя и приближенно) выборочным методом – исследователь работает с выборками и находит оценки вышеуказанных генеральных характеристик – выборочные числовые характеристики.
Выборочное среднее – это среднее арифметическое наблюдаемых значений выборки.
 , где
, где 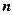 - объем выборки. (2.72)
- объем выборки. (2.72)
Если же значения 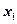 имеют соответственно частоты
имеют соответственно частоты 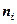 (i=1,2,…,k), причем
(i=1,2,…,k), причем 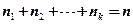 (т.е. выборка задана в виде статистического ряда), то
(т.е. выборка задана в виде статистического ряда), то
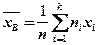 , (2.73)
, (2.73)
т.е. выборочная средняя есть средняя взвешенная значений наблюдаемого признака с весами, равными соответствующим частотам.
Выборочная дисперсияявляется оценкой генеральной дисперсии
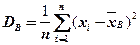 (2.74)
(2.74)
Если значения наблюдаемого признака 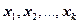 имеют соответствующие частоты
имеют соответствующие частоты 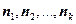 , причем
, причем 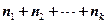 =
= 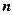 есть объем выборки, то
есть объем выборки, то
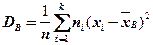 , (2.75)
, (2.75)
т.е. выборочная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.
Выборочным средним квадратическим отклонением (стандартом)называют квадратный корень из выборочной дисперсии:
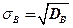 . (2.76)
. (2.76)
В дальнейшем для упрощения выкладок 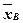 будем обозначать через
будем обозначать через 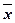 .
.
Групповая средняя – это среднее арифметическое значений наблюдаемого признака, принадлежащих группе.
Общая средняя – это среднее арифметическое значений наблюдаемого признака, принадлежащих совокупности всех групп.
Общая средняя равна средней арифметической групповых средних, взвешенной по объемам групп.
Пример.Пусть первая группа состоит из десяти элементов наблюдаемого признака со значениями равной единице и из пятнадцати элементов со значениями равной шести. Вторая группа – из 20 элементов со значениями 1 и из 30 элементов со значениями 5.
Найдем групповые средние:
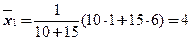 ,
, 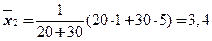 .
.
Найдем общую среднюю по групповым средним: 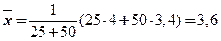 .
.
Замечание. Для упрощения расчета общей средней совокупности большого объема целесообразно разбить ее на несколько групп, найти групповые средние и по ним найти общую среднюю.
Теорема.Сумма произведений отклонений на соответствующие частоты равна нулю:
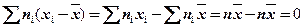 .
.
Следствие Среднее значение отклонения равно нулю:  .
.
Зачастую для вычисления 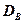 применяют следующую формулу:
применяют следующую формулу:
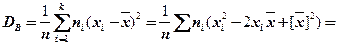
= 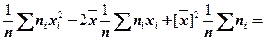
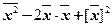 =
= 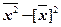 ,
,
Итак, 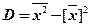 , (2.77)
, (2.77)
это формула вычисления дисперсии (безразлично – выборочной или генеральной).
При задании выборки в виде интервального статистического ряда в формулах (2.72) – (2.77) вместо 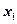 рассматриваем среднее значение
рассматриваем среднее значение 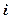 -го подыинтервала:
-го подыинтервала:
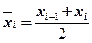 .
.
Для примера 2.8 имеем:
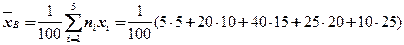 =15,75.
=15,75.
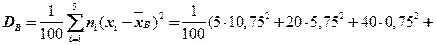
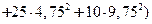 = 27,7625,
= 27,7625,
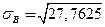 = 5,269.
= 5,269.
Для примера 2.9 имеем:
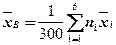 =
= 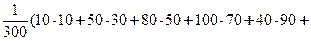
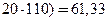 ,
,
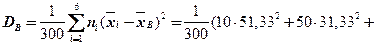
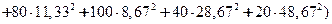 = 578,22,
= 578,22,
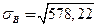 = 24,05.
= 24,05.
Дата добавления: 2016-09-20; просмотров: 1420;