Групповая, внутригрупповая, межгрупповая и общая дисперсии

Пусть совокупность (безразлично – генеральная или выборочная) разбита на 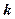групп. Каждую группу рассмотрим как самостоятельную совокупность, которая имеет свою групповую среднюю и дисперсию.

Групповая дисперсия – это дисперсия значений исследуемого (наблюдаемого) количественного признака принадлежащей группе относительно групповой средней:

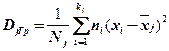, (2.78)

где 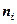- частота значения 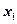; 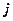- номер группы; 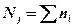- объем группы .

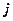Внутригрупповой дисперсиейназывают среднюю арифметическую дисперсий, взвешенную по объемам групп:

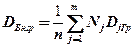, (2.79)

где 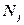- объем группы 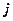; 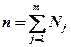- объем всей совокупности.

Межгрупповой дисперсиейназывают дисперсию групповых средних относительно общей средней:

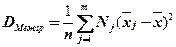(2.80)

где 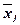- групповая средняя группы 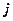; 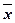- общая средняя; 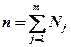объем всей совокупности.

Общей дисперсиейназывают дисперсию значений признака всей совокупности относительно общей средней:

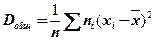. (2.81)

Пример 2.10Совокупность состоит из двух групп: первая группа содержит один элемент со значением 2, семь элементов со значениями 4 и два элемента со значениями 5, вторая группа содержит два элемента со значениями 3 и три элемента со значениями 8.

Найти а) групповые дисперсии

б) внуртигрупповую дисперсию

в) межгрупповую дисперсию

г) общую дисперсию

Решение.

а) Найдем групповые средние:

= ;

.

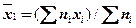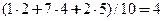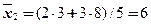Найдем искомые групповые дисперсии: 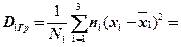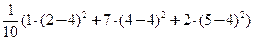= 0,6;

.

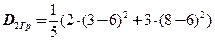б) Внутригрупповая дисперсия равна:

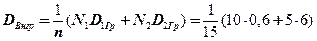= 12/5.

в) Сначала найдем общую среднюю:

.

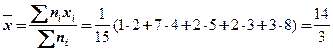Используя вычисленные групповые средние 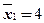, , 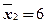найдем межгрупповую дисперсию:

.

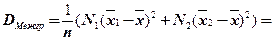
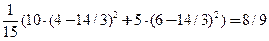г) Найдем общую дисперсию:

+ .

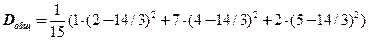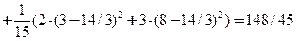Теорема.Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий:

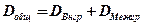(2.82)

Для вышеприведенного примера проверяем: .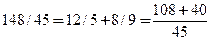

Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям:

быть несмещенные, эффективные и состоятельные.

1) Несмещенность– оценки лишь по случайному совпадению могут в точности равняться характеристикам генеральной совокупности. Обычно не совпадают, присутствует определенная ошибка. Мы хотели бы, чтобы мат. ожидание оценки равнялось соответствующей характеристике генеральной совокупности.

Несмещенной называют статистическую оценку 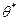, мат. ожидание которой равно оцениваемому параметру 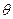при любом объеме выборки, т.е. 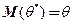. В противном случае оценку называют смещенной.

2) Эффективнойназывают статистическую оценку, которая при заданном объеме выборки 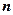имеет наименьшую возможную дисперсию среди всех несмещенных оценок.

Предположим, что на основе двух выборок одного и того же объема имеем две несмещенные оценки теоретического (генерального) среднего (см. рис. 2.15)

Рис. 2.15.

Какую оценку предпочесть: А несмещенная, но у В меньше дисперсии?

Поскольку функция плотности вероятностей для оценки 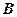более «сжата» чем для оценки 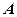, то с помощью первой мы скорее получим более точное значение. Говорят, эта оценка более эффективна.

Итак, для оценки желательно несмещенность и наименьшая возможная дисперсия (эффективность). Эти критерии иногда могут противоречить друг другу. Могут быть две оценки, одна из которых является несмещенной, другая же смещена, но имеет меньшую дисперсию, чем первая. Какую из оценок выбрать? Если вы намерены вести наблюдения за длительный период, когда возможные ошибки (отклонения) «погасят» друг друга, то выберете оценку 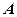. Если приемлемы малые ошибки, то выберете оценку .

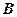Оценка называется асимптотически эффективной, если с увеличением объема выборки ее дисперсия стремится к нулю.

3) Состоятельность.Естественно полагать, что при увеличении объема выборки оценка мат. ожидания - 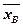становится более точной. В единичном эксперименте большая выборка необязательно даст более точную оценку, чем меньшая выборка, так как всегда может присутствовать элемент везения (случайно неудачный выбор наблюдаемых значений), но общая тенденция – большая выборка обязательно даст более точные оценки.

Если предел оценки по вероятности (обычно для описания этого факта используют символ 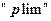, означающий «предел по вероятности») равен истинному значению характеристики ген. совокупности, то эта оценка называется состоятельной. Иначе говоря состоятельной называется такая оценка, которая дает более точные значения с увеличением объема выборки, независимо от входящих в нее конкретных наблюдений.

Оценка 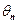параметра 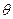называют состоятельной, если она удовлетворяет закону больших чисел, т.е. сходится по вероятности к оцениваемому параметру: , ( ).

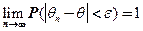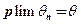Состоятельная оценка, – у которой смещение и дисперсия стремятся к нулю при увеличении объема выборки. Для малых выборок иногда невозможно найти несмещенную оценку, но если анна хотя бы состоятельна, это лучше, чем не иметь никакой оценки. На малых выборках несостоятельная оценка может иметь меньшую дисперсию, чем состоятельная, поэтому требуется осторожность при выборе данных.

Нетрудно показать, что 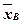является несмещенной оценкой генерального среднего, т.е. 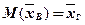. Выборочная средняя является и состоятельной оценкой генеральной средней.

Для оценки генеральной дисперсии по выборочной дисперсии умножают 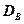на дробь 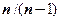(чтобы компенсировать смещенность точнчной оценки).

«Исправленную» дисперсию обычно обозначают через .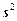

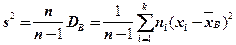. (2.83)

Для оценки среднего квадратического отклонения генеральной совокупности 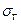используют «исправленное» среднее квадратическое отклонение - .

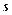Следует подчеркивать, что 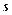не является несмещенной оценкой, поэтому слово «исправленное» взято в кавычки.

Выборочную дисперсию обозначают также через вариацию - :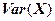

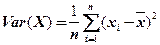, (2.84)

Выборочную дисперсию переменной 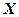обозначают и через : .

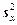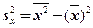Определенная таким образом выборочная дисперсия является смещенной оценкой теоретической (генеральной) дисперсии 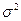: 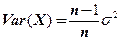и имеет отрицательное смещение. Причина в том, что она вычисляется как среднеквадратичное отклонение от выборочного среднего, а не от истинного. Так как выборочное среднее автоматически находится в центре выборки, то отклонения от него в среднем будут меньше отклонений от теоретического среднего значения.

При увеличении размера выборки 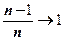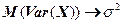или пишут 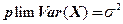, т.е. является состоятельной оценкой с отрицательным смещением для небольших выборок.

Выборочный коэффициент вариации 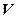определяется отношением выборочного среднего квадратического отклонения к выборочной средней, выраженным в процентах (см. ):

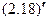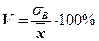. (2.85)

Коэффициент вариации – безразмерная величина, удобна для сравнения величин рассеивания двух выборок, имеющих различные размерности, например, если варианты одного ряда выражены в сантиметрах, а другого – в граммах.

Кроме выборочной средней и выборочной дисперсии применяются и другие характеристики вариационного ряда. Укажем главные из них.

Модой 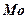называют варианту, которая имеет наибольшую частоту.

Например, для ряда:

варианта …………1 4 7 9

частота ………….5 1 20 6 мода равна 7.

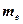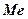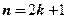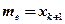Медианой (обозначают также ) называют варианту, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно, т.е. , то ; при четном 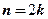медиана

.

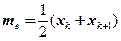Например, для ряда 2 3 5 6 7 медиана равна 5; для ряда 2 3 5 6 7 9 медиана равна(5+6)/2=5,5.

Средним абсолютным отклонением 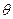называют среднее арифметическое абсолютных отклонений:

.

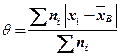Например, для ряда: варианта …….. 1 3 6 16

частота ……... 4 10 5 1 имеем:

, .

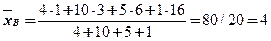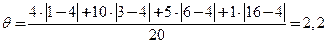Среднее абсолютное отклонение служит для характеристики рассеяния вариационного ряда.