Упражнения и задачи

1. Приведены результаты наблюдения за объемами ежедневных продаж некоторого товара за 60 дней:

5, 6, 3, 2, 7, 7, 6, 6, 10, 11, 6, 4, 5, 6, 3, 12, 9, 10, 7, 4, 6, 7, 8, 8, 10, 5, 5, 4, 3, 6, 6, 7, 7, 8, 8, 10, 6, 4, 5, 6, 12, 7, 7, 8, 11, 9, 10, 5, 6, 4, 2, 7, 11, 8, 7, 9, 5, 6, 9, 5.

Необходимо:

а) построить статистический ряд;

б) определить размах выборки;

в) построить эмпирическую функцию распределения и ее график;

г) построить полигон относительных частот;

д) определить выборочные: среднюю, дисперсию, среднее квадратическое отклонение.

е) дать интервальную оценку генеральной средней на уровне значимости 0,05.

2. Для анализа продолжительности телефонных разговоров некоторой справочной телефонной службы с клиентами случайным образом отобраны 60 телефонных разговоров и зафиксированы их длительности (в секундах):

39, 60, 40, 52, 32, 68, 77, 61, 68, 60, 47, 49, 70, 55, 66, 80, 35, 67, 70, 55, 42,

52, 60, 82, 70, 55, 47, 39, 50, 58, 45, 50, 53, 33, 49, 54, 55, 70, 62, 60, 60, 40,

59, 64, 70, 55, 54, 35, 48, 52, 57, 55, 82, 70, 51, 35, 49, 60, 55, 47.

Необходимо:

а) вычислить выборочное среднее, выборочную дисперсию, выборочное среднее квадратическое отклонение рассматриваемого признака;

б) построить интервальный статистический ряд, включающий 5 интервалов (при этом какой шаг вы выбрали и почему?);

в) построить гистограмму и по ее виду выдвинуть предположение о законе распределения рассматриваемой СВ;

г) вычислить выборочные числовые характеристики рассматриваемой величины на основании построенного интервального статистического ряда;

д) построить интервальный статистический ряд, включающий 7 интервалов и вычислить на его основе выборочные числовые характеристики рассматриваемой случайной величины;

е) сравните результаты вычислений в пунктах а), г) и д); каковы ваши выводы?

3. По имеющейся эмпирической функции распределения построить статистический ряд и полигон частот, если объем выборки .

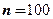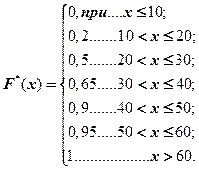
4. Анализируется размер дивидентов по акциям некоторой кампании. Для

анализа отобраны данные за последние 20 лет:

5, 10, 7, -5, 3, 10, 15, 10, 5, -3, -5, 3, 7, 15, 10, 10, 0, -2, 5, 10.

а) Каков ожидаемый размер дивидентов?

б) Как можно оценить риск от вложений в данную компанию?

5. Анализируется прибыль ( 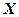) фирм в некоторой отрасли. Имеющиеся статистические данные по 100 фирмам представлены следующим интервальным статистическим рядом:

, %

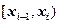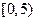
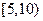
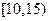
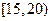
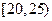
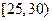
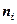
Необходимо:

а) оценить величину ожидаемой (средней) прибыли в отрасли;

б) построить гистограмму и выдвинуть предположение о виде закона распределения СВ ;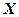

в) оценить величину относительного разброса прибылей в данной отрасли.

6.Даны результаты наблюдений цены некоторого товара в 20 магазинах: 50, 48, 47, 55, 50, 45, 50, 52, 48, 50, 52, 48, 50, 47, 50, 48, 52, 50, 50, 48.

Необходимо:

а) построить статистический ряд и полигон относительных частот;

б) определить предполагаемый вид закона распределения СВ – цены товара и оценить параметры предполагаемого закона распределения.

7. Данные наблюдений за СВ 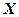(количество вновь регистрируемых фирм) и 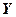(количество банкротств) за 10 лет представлены в следующей таблице:

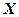
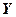
Год			Год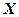

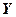
а) Каково ожидаемое количество вновь регистрируемых фирм в течение года для данного временного интервала; каковы выборочная дисперсия и среднее квадратическое отклонение для этого показателя?

б) Каково ожидаемое количество банкротств в течение года для данного временного интервала; каковы выборочная дисперсия и среднее квадратическое отклонение для этого показателя?

в) Вычислите ковариацию и коэффициент корреляции между 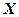и 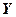. Являются ли эти переменные независимыми?

г) Есл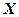и и 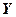коррелированны, то можно ли утверждать, что один из этих показателей является «следствием» другого, т.е. изменение одного влечет изменение другого?