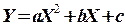Ниже для удобства аргументы ковариации записаны маленькими буквами.
- ковариация двух СВ характеризует как степень зависимости между ними, так и их рассеяние вокруг «центра тяжести»,т.е точки 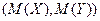 .
.
- ковариация имеет размерность (если 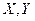 в метрах, то
в метрах, то 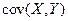 будет в
будет в 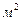 - ах), что затрудняет ее использование для оценки степени зависимости случайных величин.
- ах), что затрудняет ее использование для оценки степени зависимости случайных величин.
- коэффициент корреляции (Пирсона)двух СВ это отношение их ковариации к произведению их средних квадратических отклонений: (обозначают 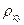 ,
, 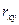 )
)
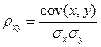 (2.69)
(2.69)
Корреляционный момент двух независимых СВ 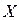 и
и  равен нулю.
равен нулю.
Коэффициент корреляции двух независимых СВ  и
и  равен нулю.
равен нулю.
Если 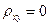 , то СВ
, то СВ  и
и  называются некоррелированными.
называются некоррелированными.
Если 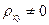 , то СВ
, то СВ  и
и  называются коррелированными.
называются коррелированными.
Свойства ковариации:
1. 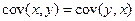 , (
, ( 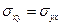 ). 2.
). 2. 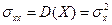 .
.
3. Для независимых СВ 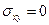 . 4.
. 4. 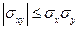 .
.
Правила
1. 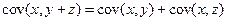 .
.
2. 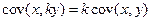 , где
, где 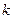 постоянная величина.
постоянная величина.
3. 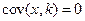 , где
, где 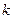 постоянная величина.
постоянная величина.
4. 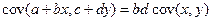 , где
, где 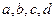 - константы.
- константы.
Свойства коэффициента корреляции:
1. 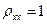 . 2.
. 2. 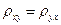 . 3.
. 3. 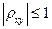 .
.
4. 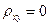 , если СВ
, если СВ  и
и  независимы (не существует никакая связь).
независимы (не существует никакая связь).
5. 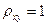 , если между
, если между 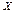 и
и  существует прямая линейная функциональная зависимость,
существует прямая линейная функциональная зависимость, 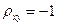 , если между
, если между 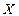 и
и  существует обратная линейная функциональная зависимость.
существует обратная линейная функциональная зависимость.
Заметим, что если 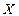 и
и  независимые СВ, то
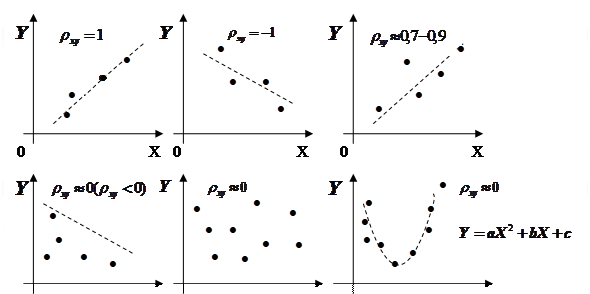
независимые СВ, то 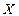 и
и  - некоррелированные СВ. Обратное утверждение неверно. Это наглядно проиллюстрировано на рис. 2.7.
- некоррелированные СВ. Обратное утверждение неверно. Это наглядно проиллюстрировано на рис. 2.7.
 |
|
|
|

Рис. 2.7
В параграфе 2.1 были приведены основные свойства и формулы расчета дисперсии (для независимых СВ). В случае, когда СВ  и
и  зависимы, т.е коррелируют друг друга, формулы расчета дисперсии их суммы или разности приобретают вид:
зависимы, т.е коррелируют друг друга, формулы расчета дисперсии их суммы или разности приобретают вид:
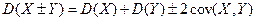 , (2.70)
, (2.70)
где по 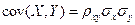 , (см. (2.69)).
, (см. (2.69)).
Значимость коэффициента корреляции при анализе данных наблюдении рассмотрим в главе 3 (регрессионный анализ) данного пособия.
Пример 2.5.Компания многие годы вложила средства в две отрасли и получала дивиденды (в процентах) от вложений. В результате многолетних наблюдений за инвестициями был построен закон распределения размеров годовых дивидентов
( СВ  и
и  ) от вложений в данные отрасли ( см. таблицу 2.5)).
) от вложений в данные отрасли ( см. таблицу 2.5)).
Необходимо определить маргинальные законы распределения каждой из СВ, установить наличие зависимости между ними. Вычислить ковариацию и коэффициент корреляции, а также решить, что менее рискованно: вкладывать деньги в одну из этих отраслей либо одновременно в обе отрасли в равных пропорциях.
Таблица 2.5

| 
| 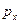
| ||
| -10 | ||||
| -10 | 0,05 | 0,25 | 0,3 | 0,6 |
| 0,15 | 0,20 | 0,05 | 0,4 | |
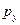
| 0,2 | 0,45 | 0,35 |
Решение: условная вероятность 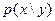 определяется по столбцам таблицы, а
определяется по столбцам таблицы, а 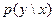 - по строкам. Например,
- по строкам. Например, 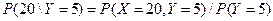 =
=
=0,2/0,45=0,444. Предельные (маргинальные) законы распределения СВ  и
и  представлены в правом столбце и нижней строке таблицы.
представлены в правом столбце и нижней строке таблицы.
Так как 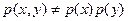
(например, 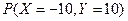 = 0,3
= 0,3 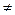 0,6
0,6  0,35 = 0,21 =
0,35 = 0,21 = 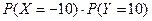 ), то СВ
), то СВ  и
и  не являются независимыми. По построенным маргинальным законам распределений СВ определим числовые характеристики
не являются независимыми. По построенным маргинальным законам распределений СВ определим числовые характеристики  и
и  :
:
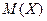 =-10
=-10  0,6+20
0,6+20  0,4 = 2;
0,4 = 2; 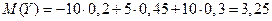 ;
;
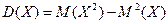 =
= 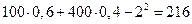 ;
;
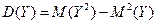 =
= 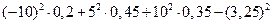 = 55,6875;
= 55,6875;
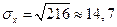 ;
; 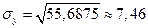 .
.
Ковариацию и коэффициент корреляции найдем по формулам:
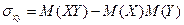 =
= 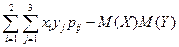 =
=
= 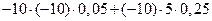
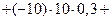
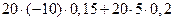 +
+
+ 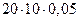
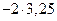
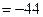
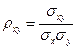
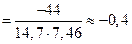 .
.
Коэффициент корреляции 0,4 говорит о том, что между СВ  и
и  (годовыми дивидендами в процентах) существует не очень сильная отрицательная линейная зависимость.
(годовыми дивидендами в процентах) существует не очень сильная отрицательная линейная зависимость.
Риски от вложений можно определить по разбросу значений их дивидентов, т.е по дисперсиям СВ. Дисперсии дивидентов  и
и  соответственно равны 216 и 55,6875, следовательно вложения в первую отрасль более рискованно, чем во вторую.
соответственно равны 216 и 55,6875, следовательно вложения в первую отрасль более рискованно, чем во вторую.
Обозначим размер годовых дивидентов (в процентах) от вложения денег одновременно в обе отрасли в равных пропорциях через Z: 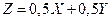 .
.
Мат.ожидание и дисперсия соответственно равны:
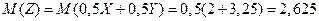 ;
;
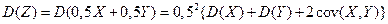 =
=
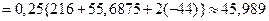 .
.
Поскольку 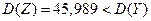 = 55,6875, то одновременное вложение в обе отрасли в равных пропорциях является наименее рискованным из трех рассмотренных вариантов инвестиций.
= 55,6875, то одновременное вложение в обе отрасли в равных пропорциях является наименее рискованным из трех рассмотренных вариантов инвестиций.
Вопросы для самопроверки
1. Приведите примеры случайных событий в экономике.
2. Что такое относительная частота события, как она связана с вероятностью?
3. Что такое случайная величина (СВ)? Какие виды СВ известны?
4. Приведите примеры дискретных и непрерывных СВ из экономики.
5. Перечислите основные числовые характеристики СВ. Как они вычисляются
6. для дискретных и непрерывных СВ?
7. Что такое функция распределения вероятностей СВ? Что такое плотность распределения ? Приведите их свойства.
8. Каким образом может быть задана СВ.
9. Как рассчитывается вероятность попадания СВ в определенный интервал с помощью функции распределения, с помощью плотности распределения?
10. Выведите основные свойства мат. ожидания и дисперсии, используя их определения.
11. Как связаны между собой СВ, имеющие стандартизированное нормальное распределение, распределения Стьюдента, Хи Квадрат и Фишера?
12. К какому распределению стремятся распределения Стьюдента, Хи Квадрат и Фишера при увеличении числа степеней свободы?
13. Что такое ковариация (корреляционный момент) и коэффициент корреляции? Перечислите их свойства.
14. Что такое двумерная (многомерная) СВ, закон ее распределения, условная вероятность и двумерная плотность распределения?
15. Что такое независимость двух СВ, как определяется коррелированность СВ?
Дата добавления: 2016-09-20; просмотров: 899;