Упражнения и задачи. 1.На основе многочисленных наблюдений установлено, что доля покупателей-женщин в данном парфюмерном магазине составляет 70%
1.На основе многочисленных наблюдений установлено, что доля покупателей-женщин в данном парфюмерном магазине составляет 70%. Среди покупателей-мужщин 70% предпочитают парфюмерный товар фирмы А, а среди покупателей-женщин товары этой же фирмы предпочитают 50%. Какова вероятность того, что случайный покупатель предпочтет товар фирмы А?
2. Семь из десяти посетителей кафе заказывают к кофе пирожное. Два человека заказывают кофе. Какова вероятность того, что они закажут: а) два пирожных; б) одно пирожное; в) ни одного пирожного?
3. Брокер может приобрести акции одной из четырех компаний А, В, С, D. Риски прогореть при покупке акций этих компаний соответственно составляют 50%, 40%, 20% и 30%. Брокер решает вложить все деньги в акции одной случайно выбранной компании. Какова вероятность того, что брокер прогорит?
4. Совет директоров компании состоит из 12 человек; 3 из них лоббируют проект А, 5 – проект В, а остальные склонны инвестировать деньги в проект С. Решение об инвестировании будет принимать большинством голосов комиссия, состоящая из 5 выбранных жребием директоров. Какова вероятность принятия решения в пользу проекта В?
5. Исследуется динамика курсов валют А и В по отношению к валюте С. Статистика торгов на валютной бирже свидетельствует, что при возрастании курса валюты В курс валюты А растет в 80% случаев, при снижении курса валюты В курс валюты А растет в 25% случаев, при неизменности курса валюти В курс валюты А растет в 50% случаев. Предполагая, что варианты изменения курса валюты В равновозможны, определить вероятности соответствующих изменений при условии, что на последних торгах курс валюты А вырос.
6. Среди 10000 лотерейных билетов 10% являются выигрышными. Определить:
а) вероятность выигрыша при покупке 5 билетов;
б) количество билетов, которое необходимо приобрести, чтобы выиграть с вероятностью 0,9;
в) что вероятнее: выиграть или не выиграть при покупке 7 билетов?
7. Задан закон распределения дискретной СВ Х:

| |||||
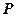
| b | 2b | 3b | 4b | 5b |
Определить:
а) значение b;
б) значения 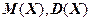 ;
;
в) вероятность 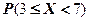 .
.
8. Известно распределение годовой прибыли  фирмы:
фирмы:

| -10 | -5 | ||||
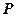
| 0,05 | 0,15 | 0,25 | 0,30 | 0,20 | 0,05 |
Необходимо определить ожидаемую прибыль, среднее квадратическое
отклонение. Определите вероятность положительной прибыли.
9. СВ  - величина ежемесячного спроса на некоторый продукт – задана следующим законом распределения:
- величина ежемесячного спроса на некоторый продукт – задана следующим законом распределения:

| ||||||
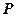
| 0,05 | 0,15 | 0,25 | 0,30 | 0,20 | 0,05 |
Издержки на производство единицы продукции составляют 5$, продукция продается по фиксированной цене 10$ за единицу. Целью производителя является максимизация ожидаемой прибыли. Какова величина ожидаемой прибыли и ее дисперсии?
10. Проведен маркетинговый анализ количества автомобилей района для определения целесообразности строительства станции техобслуживания.
Обследовано 5000 семей. Из них в 250 автомобили отсутствовали, а в 1500 было по 1 автомобилю, в 2500 – по 2, в 600 – по 3 и в 150 по 4. Вероятность поломки автомобиля равна 0,05. Станция будет рентабельна, если ее ежедневная загрузка составит 5 автомобилей. Целесообразно ли строительство станции в данном районе?
11. СВ  имеет плотность вероятности
имеет плотность вероятности 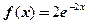 при
при 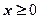 и
и 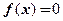 при
при
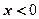 . Найти вероятность того, что СВ при четырех испытаниях попадет в
. Найти вероятность того, что СВ при четырех испытаниях попадет в
интервал от 0 до 1 ровно три раза.
12. Двумерная СВ 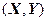 задана следующим законом распределения:
задана следующим законом распределения:

| 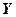
| |||
| -10 | ||||
| 0,25 | 0,10 | 0,15 | 0,00 | |
| 0,00 | 0,05 | 0,30 | 0,15 |
а) Определить маргинальные законы распределений СВ  и
и 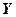 ,
,
б) Вычислить ожидаемые значения  и
и 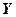 , а также их дисперсии.
, а также их дисперсии.
в) Определить условные вероятности 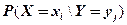 и
и 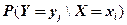 .
.
г) Являются ли СВ  и
и 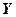 независимыми?
независимыми?
13. СВ  и
и 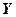 - годовые дивиденды от вложений в отрасли А и В соответственно. Риск от вложений характеризуется дисперсиями:
- годовые дивиденды от вложений в отрасли А и В соответственно. Риск от вложений характеризуется дисперсиями:  =16,
=16, 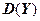 =9. Коэффициент корреляции
=9. Коэффициент корреляции 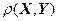 = -0,6. Что менее рискованно, вкладывать в обе отрасли в соотношении 30% на 70% или только в отрасль В?
= -0,6. Что менее рискованно, вкладывать в обе отрасли в соотношении 30% на 70% или только в отрасль В?
14.Имеются три вида акций А, В и С, каждая стоимостью 10$, дивиденды по акциям независимые случайные величины (СВ) со средним значением 10% и дисперсией 16 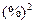 . Формируются два портфеля инвестиций:
. Формируются два портфеля инвестиций: 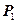 - из 30 акций А и
- из 30 акций А и 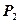 - включает в себя по 10 акций А,В и С.
- включает в себя по 10 акций А,В и С.
а) Отличаются ли данные портфели по величинам ожидаемых дивидендов и по риску?
б) Пусть коэффициент корреляции между дивидендами по акциям А и В равен -0,5 , но обе эти величины не коррелируют с дивидендами по акциям С. Как это отразится на ответе на вопрос а)?
в) Если дивиденды по рассматриваемым акциям положительно коррелированны друг с другом, то снизит ли риск вложений покупка различных акций?
г) Если корреляция между акциями А и В является совершенной отрицательной, то что можно ожидать при формировании портфеля по принципу 50% акций А и 50% акций В?
15. Доход Х населения имеет нормальный закон распределения со средним значением 1000$ и средним квадратическим отклонением 400$. Обследуется 1000 человек. Какое количество человек будет иметь доход более 1500$? Назовите наиболее вероятное количество.
16.Прибыль в отрасли имеет нормальный закон распределения со средним значением 1 млн$ и средним квадратическим отклонением 0,25 млн$. Что вероятнее, получить прибыль не более чем 0,8 млн$ или в пределах от 1,2 млн$ до 1,5 млн$?
Дата добавления: 2016-09-20; просмотров: 2374;
