Условные законы распределения составляющих системы дискретных СВ и системы непрерывных СВ

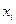Рассмотрим дискретную двумерную СВ (см. табл.2.2). Обозначим условную вероятность того, что примет значение при условии, что 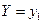, через 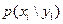. В общем случае условные вероятности составляющей обозначены так:

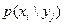, где ; .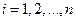

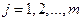Условным распределением составляющей при 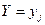называют совокупность условных вероятностей 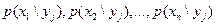, вычисленных в предположении, что событие 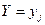( 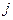фиксировано при всех значениях ) уже наступило. Аналогично определяется условное распределение составляющей . Зная закон распределения двумерной дискретной СВ, можно, пользуясь формулой (2.53) , вычислить условные законы распределения составляющих. Например, условный закон распределения в предположении, что событие 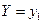уже произошло, может быть найден по формуле

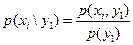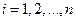( ). В общем случае условные законы распределения составляющей определяются соотношением

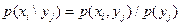(2.58)

Аналогично, условные законы распределения составляющей определяются соотношением

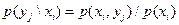(2.59)

Замечание. При фиксированно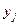м имеем 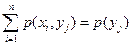, следовательно

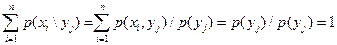(2.60)

Аналогично получим

.

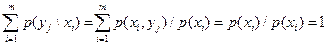Это свойство условных распределений используют для контроля вычислений.

Пример 2.3.Дискретная двумерная СВ задана таблицей 2.3

Таблица 2.3

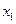
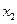
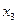
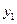
	0,20	0,30	0,15
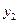
	0,05	0,10	0,20

Найдем условный закон распределения составляющей при условии, что составляющая приняла значение .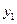

Решение. Искомый закон определяется совокупностью следующих условных вероятностей: 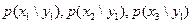. Воспользовавшись формулой (2.61) и приняв во внимание, что

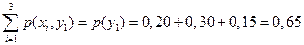, получим

,

,

.

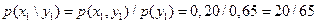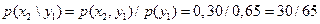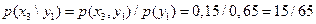Для контроля сложив найденные условные вероятности, убеждаемся, что их сумма равна единице.

Пусть 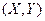- непрерывная двумерная СВ, а 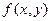ее двумерная плотность вероятностей. Нам интересует функция плотности при фиксированной одной СВ. В этом случае функция усредняется (интегрируется) по лишней переменной. В результате получается так называемая маргинальная(лат. предельная) функция плотности распределения.

Условной плотностью распределения составляющих при данном значении 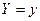(составляющих при данном значении 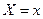) называют отношение плотности совместного распределения 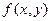системы СВ 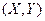к плотности распределения 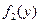составляющей (к 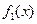составляющей ):

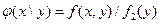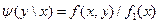, ( ) (2.62)

Для плотностей условных распределений использую также обозначения

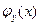и .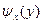

Напомним, что условная плотность 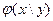отличается от безусловной плотности 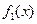тем, что дает распределение при условии, что составляющая приняла значение 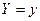; вторая же - 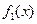дает распределение независимо от того, какие из возможных значений приняла составляющая . Условные плотности выражаются через плотность совместного распределения по формулам:

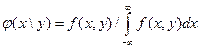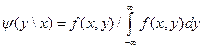, (2.63)

Формулы (2.57) запишем в виде

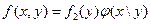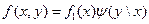, (2.64)

Следовательно, умножая закон распределения одного составляющего на условный закон распределения другой составляющей, получим закон распределения системы случайных величин.

Свойства условных плотностей распределения:

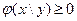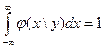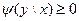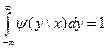, ; , (2.65)

Условное математическое ожидание(обозначают , )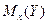

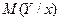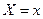Условным мат.ожиданием дискретной СВ при называют сумму произведений возможных значений на их условные вероятности:

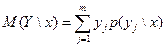(или 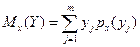) (2.66)

Для непрерывных СВ:

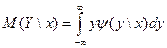. (или )

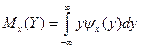Условное математическое ожидание 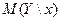есть функция от 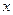, которую называют функцией регрессии на (т.е. функциональная зависимость между 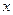и среднеожидаемым -ом ). Аналогично определяются условное мат.ожидание СВ и функция регрессии на :

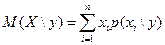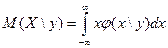, (2.67)

Используют также обозначения 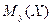и .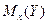

Пример 2.4. Дискретная двумерная СВ задана табл. 2.4.

Таблица 2.4

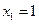
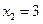
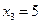
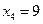
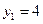
	0,15	0,06	0,25	0,04
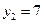
	0,30	0,10	0,03	0,07

Найдем условное мат.ожидание составляющей при : =? ( =?).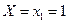

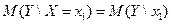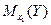Решение. = ,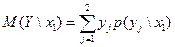

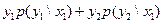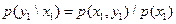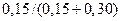= =15/45=1/3,

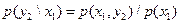=0,30/(0,15+0,30)=30/45=2/3,

Находим условное мат.ожидание 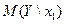=4(1/3)+7(2/3)=18/3=6.

Две СВ называем независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. Из этого определения следует, что условные распределения независимых СВ равны их безусловным распределениям.

Теорема. Для того чтобы СВ и были независимыми, необходимо и достаточно, чтобы функция распределения вероятностей системы СВ 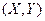была равна произведению функций распределения составляющих: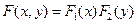

Следствие. Для того чтобы непрерывные СВ и были независимыми, необходимо и достаточно, чтобы плотность совместного распределения системы 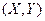была равна произведению плотностей распределения составляющих: .

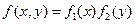Если СВ и независимы, то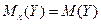

Числовыми характеристиками системы двух случайных величин являются:

- корреляционный момент (ковариация(co-vary – «совместное изменение») )(используют обозначения 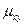, , 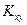, 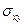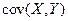) - это мат.ожидание произведения отклонений этих величин от своих мат. ожиданий:

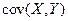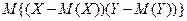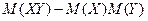= = (2.68)