Многомерные случайные величины. Понятие условного распределения.
Многие экономические показатели описываются не одной, а двумя или более случайными величинами X, Y, Z, …, W, являясь по сути многомерными СВ. Например, издержки предприятия включают в себе фиксированную и переменную составляющие. Уровень жизни населения подразумевает использование большого числа показателей: среднедушевой доход, минимальная зарплата, минимальная потребительская корзина, продолжительность жизни, наличие товаров и услуг и т.д.
Принято совокупность таких показателей назвать системой случайных величин и обозначить (X, Y, Z, …, W). Свойства системы СВ образуются не только свойствами входящих в систему отдельных СВ, но и их взаимосвязями.
Для простаты изложения ограничимся рассмотрением систем только двух СВ. Такие двумерные СВ (Х, У) удобно рассматривать как случайную точку на плоскости с координатами Х и У.
Законом распределения вероятностейдвумерной СВ называют перечень возможных значений этой величины (т.е. пар чисел 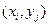 ) и их вероятностей
) и их вероятностей 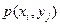 ( где
( где 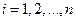 ;
; 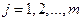 ). Обычно закон распределения задают в виде таблицы:
). Обычно закон распределения задают в виде таблицы:
Таблица 2.2

| 
| |||||
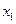
| 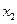
| … | 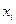
| … | 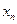
| |
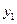
| 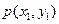
| 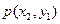
| … | 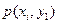
| … | 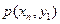
|
| … | … | … | … | … | … | … |
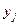
| 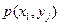
| 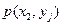
| … | 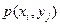
| … | 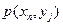
|
| … | … | … | … | … | … | … |
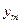
| 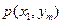
| 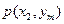
| … | 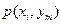
| … | 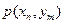
|
Зная закон распределения двумерной дискретной СВ, можно найти законы распределения каждой из составляющих. Например, события 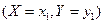 ,
, 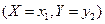 , … ,
, … , 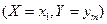 несовместны, поэтому вероятность того, что
несовместны, поэтому вероятность того, что  примет значение
примет значение 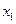 , по теореме сложения равна:
, по теореме сложения равна:
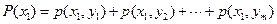 (2.52)
(2.52)
В общем случае, для того чтобы найти вероятность 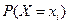 , надо просуммировать вероятности столбца
, надо просуммировать вероятности столбца 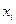 . Аналогично сложив вероятности «строки
. Аналогично сложив вероятности «строки 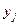 », получим вероятность
», получим вероятность 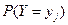 .
.
- Функцией распределения вероятностей системы двух СВназывается вероятность совместного выполнения двух неравенств 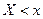 и
и 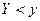 :
:
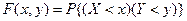 (2.53)
(2.53)
В геометрической интерпретации это есть вероятность случайного попадания материальной точки одновременно левее, чем абсцисс 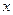 и ниже чем ордината
и ниже чем ордината 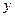 .
.
Из определения функции распределения следуют еесвойства:
1) 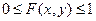 .
.
2) Функция распределения 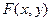 является неубывающей функцией обоих своих аргументов:
является неубывающей функцией обоих своих аргументов: 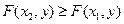 при
при 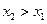 ;
; 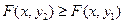 при
при 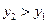 .
.
3) Имеют место предельные соотношения:
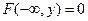 ,
, 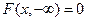 ,
, 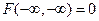 ,
, 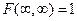 .
.
4) При 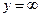 функция распределения системы
функция распределения системы 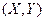 становится функцией распределения составляющей
становится функцией распределения составляющей  :
: 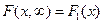 .
.
При 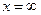 функция распределения системы
функция распределения системы 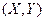 становится функцией
становится функцией
распределения составляющей  :
: 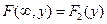 .
.
Вероятность попадания случайной точки 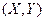 в полуполосу:
в полуполосу:
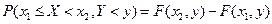 ,
, 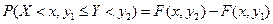 .
.
Таким образом, вероятность попадания случайной точки в полуполосу равна приращению функции распределения по одному из аргументов.
Вероятность попадания случайной точки 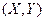 в прямоугольник с вершинами
в прямоугольник с вершинами 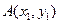 ,
, 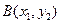 ,
, 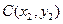 ,
, 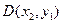 :
:
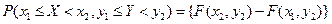 -
- 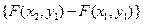 .
.
Пусть функция распределения вероятностей 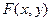 всюду непрерывна и имеет непрерывные частные производные второго порядка.
всюду непрерывна и имеет непрерывные частные производные второго порядка.
Плотностью совместного распределения вероятностей 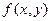 непрерывной двумерной СВ
непрерывной двумерной СВ 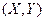 (двумерной плотностью вероятностей)называют вторую смешанную частную производную от функции распределения:
(двумерной плотностью вероятностей)называют вторую смешанную частную производную от функции распределения:
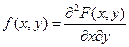 (2.54)
(2.54)
Геометрически функцию 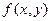 можно истолковать как поверхность в декартовой системе
можно истолковать как поверхность в декартовой системе 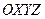 , ее называют поверхностью распределения.
, ее называют поверхностью распределения.
Зная плотность совместного распределения 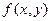 , можно найти функцию распределения
, можно найти функцию распределения
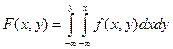 (2.55)
(2.55)
Произведение 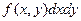 (при малых приращениях
(при малых приращениях 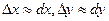 ) есть вероятность
) есть вероятность 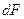 попадания случайной точки
попадания случайной точки 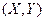 в прямоугольник со сторонами
в прямоугольник со сторонами 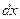 и
и 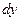 . Тогда вероятность попадания случайной точки в произвольная область D равна двойному интегралу по области D от функции
. Тогда вероятность попадания случайной точки в произвольная область D равна двойному интегралу по области D от функции 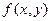 :
:
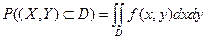 (2.56)
(2.56)
Геометрически эту вероятность можно истолковать как объем тела – вертикальной колонны, ограниченного сверху поверхностью 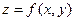 , основанием которого служит проекция этой поверхности на плоскость
, основанием которого служит проекция этой поверхности на плоскость 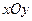 , т.е. область D.
, т.е. область D.
Свойства двумерной плотности вероятности:
1. 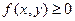 .
.
2. 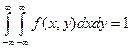 .
.
Дата добавления: 2016-09-20; просмотров: 955;
