Предельные теоремы теории вероятностей. Закон больших чисел.

В этом параграфе приведены основные сведения о законах больших чисел и центральной предельной теореме. Законы больших чисел утверждают, что среднее арифметическое большого числа независимых СВ ведет себя как среднее арифметическое их математических ожиданий.

Согласно центральной предельной теореме большая сумма малых СВ ведет себя приближенно как нормальная СВ.

Эти утверждения имеют большое практическое значение и составляют теоретическую основу математической статистики, широко применяющейся для анализа экономической информации (результатов наблюдении) с целью выработки обоснованных управляющих решений.

Анализируя собранную экономическую информацию и определив закон распределения СВ, все же нельзя уверенно прогнозировать, предвидеть ее дальнейшие значения, потому что на явление (процесс) влияют многие неучтенные в модели (по причине наших незнании о их существовании или нашей неспособности их учета) факторы, причины. Оказывается, что при достаточно большого числа случайных величин (СВ), хоть и каждое из них имеет стохастическое, хаотическое поведение, суммарное поведение всего ансамбля почти утрачивает случайный характер и становится почти закономерным.

Для практики очень важно знать, при каких условиях совокупное влияние большого числа случайных причин (величин) приводит к результату, почти не зависящему от случая (от каждого из них), т.е. позволяет прогнозировать ход явлений. Эти условия приводятся в виде теорем, основное из которых теорема Чебышева (в частном случае теорема Бернулли).

Теоретическую основу законов больших чисел составляют понятие сходимости СВ по вероятности и неравенство Чебышева.

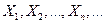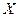Сходимость по вероятности последовательности СВ к СВ означает, что при 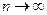вероятность приближенности 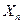к 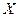стремится к единице: .

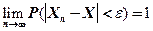По теореме Чебышева среднее арифметическое большого числа независимых СВ (дисперсии которых равномерно ограничены, т.е. не превышают постоянного числа С) ведет себя как среднее арифметическое их математических ожиданий ( тем точнее, чем больше независимых « участников» - СВ):

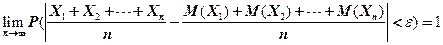(2.48)

Формулируя теорему Чебышева, предполагали, что СВ имеют различные мат. ожидания. На практике часто СВ имеют одинаковые мат. ожидания – обозначим через 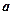, следовательно их среднее арифметическое также равно 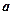. Для этого частного случая теорема Чебышева формулируется так:

Если 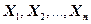- попарно независимые случайные величины, имеющие одно и то же мат. ожидание 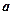, и если дисперсии этих величин равномерно ограничены, то, как бы мало не било число 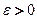, вероятность неравенства

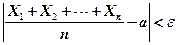
будет как угодно близка к единице, если число СВ 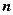достаточно велико.

Другими словами будет иметь место равенство:

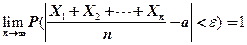(2.49)

Сущность теоремы такова: хотя отдельные независимые СВ могут принимать значения, далекие от своих мат. ожиданий, среднее арифметическое достаточно большого числа СВ с большой вероятностью принимает значения, близкие среднему арифметическому их мат. ожиданий. Иными словами, отдельные СВ могут иметь значительный разброс, а их среднее арифметическое имеет малый разброс.

Таким образом, нельзя уверенно предсказать, какое возможное значение примет каждая из СВ, но можно предвидеть, какое значение примет их среднее арифметическое.

Среднее арифметическое достаточно большого числа независимых СВ (дисперсии которых равномерно ограничено) почти утрачивает характер СВ. Объясняется это тем, что отклонения каждой из СВ от своих мат. ожиданий могут быть как положительными, так и отрицательными, а в среднем арифметическом они взаимно погашаются.

Значение теоремы Чебышева для практики велико. Широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят о всей совокупности исследуемых объектов, основан на теореме Чебышева.

Например, определение качества зерна по небольшой его пробе. Число наудачу отобранных зерен мало сравнительно со всей массой зерна, но само по себе оно достаточно велико, чтобы судить о качестве всей совокупности. Обычно для измерения некоторой физической величины производят несколько измерений и в качестве искомого размера берут их среднее арифметическое, тем самим минимизируя случайные отклонения измеряемой величины. Однако ошибочно думать, что, увеличивая число измерений, можно достичь сколь угодно большой точности. Дело в том, что все измерения получаются лишь с точностью, не превышающей точности (чувствительности) прибора.

Пусть производится 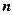независимых испытаний, в каждом из которых вероятность появления события А равна . Можно ли предвидеть, какова примерно будет относительная частота появлений события? Положительный ответ на этот вопрос дает теорема Якоба Бернулли (доказана им и опубликована в 1713 г.), которая получила название «закона больших чисел» и положила начало теории вероятностей как науке.

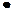Теорема Бернулли.Если в каждом из 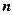независимых испытаний вероятность появления события А постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.

Иными словами имеет место равенство:

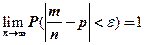(2.50)

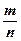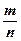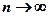Сходимость относительной частоты к вероятности отличается от сходимости в смысле математического анализа. стремится к по вероятности при , означает, что не для всех значений 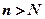(где 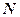большое число) неуклонно выполняется неравенство , т.е. для отдельных значений 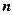неравенство может не выполняться.

Как видим, теорема Бернулли объясняет, почему относительная частота при достаточно большом числе испытаний обладает свойством устойчивости и оправдывает статистическое определение вероятности (см. гл. 1.).

Понятие о теореме Ляпунова (центральная предельная теорема)Известно, что нормально распределенные СВ широко распространены. Чем это объясняется? Ответ на этот вопрос был дан выдающимся русским математиком А.М. Ляпуновым:

теорема – если СВ Х представляет собой сумму большого числа взаимно независимых СВ, влияние каждого из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.

На практике эта теорема наиболее часто используется в том случае, когда члены суммы имеют одинаковое распределение.

Следствие из теоремы Ляпунова – Если независимые СВ 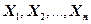имеют одинаковое распределение ( 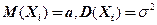), то функция распределения их центрированной и нормированной суммы 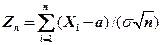сходится к функции распределения стандартной нормальной СВ:

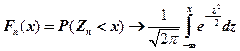(2.51)

Этим положением пользуются при решении практических задач: при 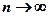распределение соответствующей суммы заменяют на распределение стандартной нормальной СВ.

Пример 2.2Определить вероятность того, что средняя продолжительность 100 производственных операций окажется в пределах от 46 до 49 с, если мат. ожидание одной операции равно 47,4 с, а среднее квадратичное отклонение – 4,9 с.

Решение – в этой задаче СВ Х это продолжительность наугад взятой операции, причем 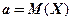=47,4 с, 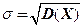=4,9 с, 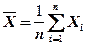, ( 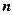=100 ) – средняя продолжительность одной операций и 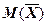=47,4 с, = .

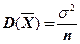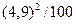
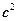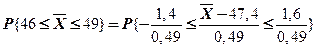
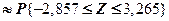= Ф(3,265)+ Ф(2,857) = = 0,9984 (воспользовались таблицей значении функции Лапласа).