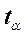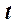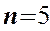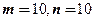Распределение Стьюдента ( t распределение)
Имеем две СВ, одна из которых распределена по стандартно-нормальному закону 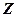 ~
~ 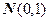 , а другая – по закону «хи квадрат» с
, а другая – по закону «хи квадрат» с 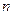 степенями свободы
степенями свободы 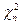 . Тогда распределением Стьюдента (или
. Тогда распределением Стьюдента (или 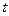 - распределением) называется распределение следующей СВ:
- распределением) называется распределение следующей СВ:
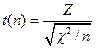 , (2.44)
, (2.44)
Функция плотности распределения Стьюдента (псевдоним английского статистика В. Госсета) имеет вид:
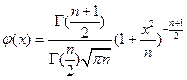 (2.45)
(2.45)
При 
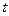 - распределение приближается к нормальному, а плотность сходится к плотности распределения стандартной нормальной СВ. Практически уже при
- распределение приближается к нормальному, а плотность сходится к плотности распределения стандартной нормальной СВ. Практически уже при 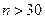
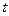 - распределение приближенно нормальное.
- распределение приближенно нормальное.
График функции плотности вероятностей СВ, имеющей распределение Стьюдента, симметричен относительно оси ординат 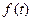 (рис. 2.5). Кривые плотности распределения Стьюдента и стандартного нормального распределения, с двусторонними критическими границами этих распределений приведены на рис. 2.5. Как видно, двусторонние критические границы распределения Стьюдента
(рис. 2.5). Кривые плотности распределения Стьюдента и стандартного нормального распределения, с двусторонними критическими границами этих распределений приведены на рис. 2.5. Как видно, двусторонние критические границы распределения Стьюдента 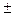
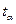 шире соответствующих границ стандартно-нормального распределения
шире соответствующих границ стандартно-нормального распределения 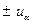 (
( 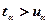 ).
).
|
|

Рис. 2.5
Распределение Стьюдента применяется для нахождения интервальных оценок, а также при проверке статистических гипотез (при этом используется таблица критических точек распределения Стьюдента, см. Пр.3).
2.2.5. Распределение Фишера–Снедекора (F-распределение)
Пусть имеем две СВ распределенные по закону «хи квадрат» 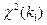 и
и 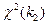 со степенями свободы
со степенями свободы  и
и 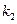 соответственно. Тогда следующая СВ:
соответственно. Тогда следующая СВ:
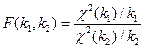 (2.46)
(2.46)
называется СВ с F- распределением (т.е. распределением Фишера) с  и
и 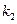 степенями свободы (обозначают также через
степенями свободы (обозначают также через 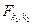 ) . Как видим, F- отношение положительная СВ. При больших
) . Как видим, F- отношение положительная СВ. При больших  и
и 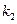 это распределение приближается к нормальному (рис.2.6). Заметим, что
это распределение приближается к нормальному (рис.2.6). Заметим, что 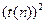 (где
(где 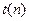 - СВ, имеющая распределение Стьюдента с числом степеней свободы
- СВ, имеющая распределение Стьюдента с числом степеней свободы 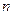 ) совпадает с F-распределением со степенями свободы 1,
) совпадает с F-распределением со степенями свободы 1, 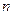 -
- 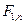 . Числовые характеристики распределения Фишера:
. Числовые характеристики распределения Фишера:
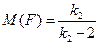
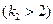 ,
, 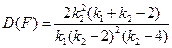
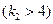 (2.47)
(2.47)
На графике изображены распределения Фишера для различных степеней свободы.
|

Рис. 2.6
Распределение Фишера используется при проверке статистических гипотез, в дисперсионном и регрессионном анализах. В таблице Пр.5. приводятся правосторонние критические границы 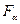 этого распределения для разных значений степеней свободы:
этого распределения для разных значений степеней свободы: 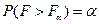 .
.
Дата добавления: 2016-09-20; просмотров: 1103;

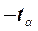
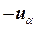 0
0