Некоторые распространенные модели распределения случайных величин

Поведение разных экономических (и не только) показателей и характеристик очень многообразно. Все же рассматриваются определенные типы поведения, которым и называют моделями законов распределения СВ и большинство разнообразных СВ ведут себя почти в рамках того или иного типа («придерживаются» определенному закону распределения). Зная закон распределения СВ можно предвидеть вероятности попадания исследуемой СВ в определенные интервалы. При анализе экономических показателей такие прогнозы весьма желательны, потому что дают возможность осуществлять продуманную политику с учетом вариантов развития ситуации.

Законов распределения достаточно много. Мы рассмотрим наиболее часто используемые в эконометрике распределения СВ. К их числу относятся нормальное распределение, распределение 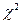(хи квадрат), распределение Стьюдента, распределение Фишера. Для удобства использования данных законов были разработаны таблицы так называемых критических точек, которые позволяют быстро и эффективно оценивать соответствующие вероятности.

Биномиальное распределение и распределение Пуассона уже рассмотрены выше. Добавим лишь, что для Пуассоновского распределения числовые характеристики СВ вычисляются по формулам:

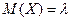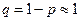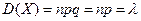, (т.к. , ) (2.31)

2.2.1. Показательный закон распределения СВ –в аналитической теории массового обслуживания время обслуживания заявок обслуживающим каналом принимается распределенным по показательному закону. Плотность распределения вероятностей имеет вид:

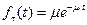, при 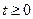и равна нулю, при 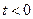, (2.32)

где 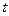- время, 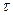- время обслуживания одной заявки (есть СВ), 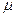- среднее число заявок, обслуженных в единицу времени, т.е. интенсивность обслуживания.

Функция распределения вероятностей имеет вид:

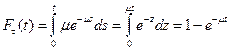(2.33)

В теории массового обслуживания часто надо знать вероятность того, что обслуживание будет продолжаться более длительное время, чем t:

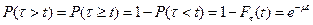(2.34)

Среднее время обслуживания одной заявки, т.е. мат. ожидание и дисперсия показательной случайной величины соответственно имеют вид :

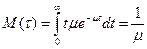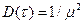, . (2.35)