Критические границы

это понятие широко используется в мат. статистике при построений доверительных интервалов и критериев проверки гипотез. Различают левосторонние, правосторонние и двусторонние критические границы.

- Левосторонней критической границей, или квантилью, отвечающей (соответствующей) вероятности , называется такая граница (т.е. значение СВ обозначенное ), левее которой вероятность равна (см. рис. 2.1) 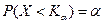. По определению это значение функции распределения вероятностей , т.е. квантиль является решением этого уравнения. Графически это означает найти такое значение СВ, левее которого площадь под графиком функции 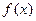равна :

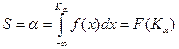. (2.26)

- Аналогично определяется правосторонняя критическая граница:

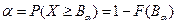(2.27)

Из определении следует, что между левосторонней и правосторонней критическими границами существует соотношение: .

- Двусторонними критическими границами, отвечающими вероятности , называют такие границы 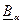и 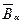, для которых СВ попадает в интервал 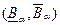с вероятностью

1- , а вне интервала попадает с вероятностью , причем

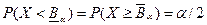. (2.28)

Двусторонние границы являются решением уравнений:

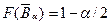. (2.29)

Для стандартного нормального распределения СВ двусторонние границы симметричны и имеют специальные обозначения: 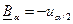и 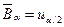, причем 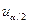является решением уравнения:

, где 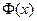- функция Лапласа.

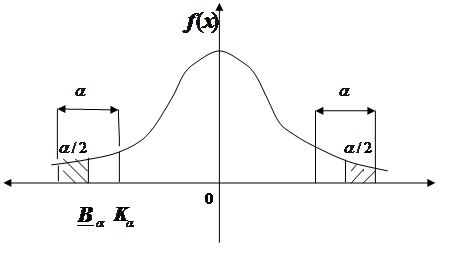
Рис. 2.1

На рис. 2.1 показаны левосторонняя и правосторонняя границы.

Мат. ожидание, мода и медиана основные характеристики положения СВ.

Дисперсия D(Х)для непрерывных СВ рассчитывается по формуле

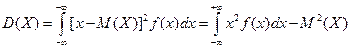(2.30)