Непрерывные случайные величины. Функция распределения (вероятностей).
Элементы теории вероятностей и математической статистики
Основные понятия и определения.
Событие –этоинтересующее нас явление в вероятностном эксперименте (наблюдении), которое может наблюдаться на исходе. Любое утверждение о появлении (или не появлении) интересующего нас параметра (явления) в конце вероятностного эксперимента (наблюдения) берут в ковички и обозначают латинской большой бкувой с начала альфавита (А,В,С,D и т.д.).
Например: имеем собитие А - «Завтра будет солнечно и занятий не будет».
Собитий можно подразделить на три вида: достоверные, невозможные и случайные.
Случайное событие– событие, которое может произойти или не произойти в условиях данного эксперимента (наблюдения).
С другой точки зрения собития подразделяются на элементарные и сложные.
Элементарное событие (исход) –любой возможный результат (исход) испытания (вероятностного эксперимента), который не подразделяется на другие события.
Пример сложного собития есть собитие А, которое можно делить на две элементарные собития; «Завтра будет солнечно» и «завьра занятий не будет».
Несовместимые события –которые не могут происходить одновременно (не могут появляться, наблюдаться совместно на исходе). Например, при однократном выбрасываний игральной кости возможны 6 равновозможные элементарные исходы (обозначим А1, А2, А3, А4, А5, А6). Любие два из них не совместные собитя.
Те элементарные исходы, в которых (с которыми) интересующее нас событие наступает, назовем благоприятствующими(способствующими) этому событию.
Несколько событий образуют полнуюгруппу, если в результате испытания появится хотя бы одно из них.
Если события, образующие полную группу, попарно несовместны, то в результате испытания появится одно и только одно из этих событий.
Вероятность события – количественная мера степени возможности его появления (осуществления) в вероятностном эксперименте (наблюдении).
Классическое определение вероятности –вероятностью появления события А называют отношение числа благоприятствующих наступлению этого события исходов (m) к общему числу всех равновозможных несовместных элементарных исходов (n), образующих полную группу.
Вероятность события А определяется формулой Р(А)=m/n ;
Классическое определение вероятности предполагает, что число элементарных исходов испытания конечно. На практике же часто встречаются испытания, число возможных исходов которых бесконечно. В таких случаях классическое определение неприменимо.
Наиболее слабая сторона классического определения состоит в том, что очень часто невозможно представить результат испытания в виде совокупности элементарных событий. Еще труднее указать основания, позволяющие считать элементарные события равновозможными. Обычно о равновозможности говорят из соображений симметрии (или однородности). По этой причине наряду с классическим определением вероятности используют и другие определения, например статистическое определение.
Одно из основных понятий теории вероятностей:
Относительная частота события – это отношение числа испытаний, в (при) которых событие появилось (это число называется частотой появления события), к общему числу фактически произведенных испытаний: 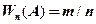 .
.
При небольшом числе экспериментов частота носит случайный характер.
При увеличении числа экспериментов случайные обстоятельства, свойственные каждому отдельному эксперименту, в массе взаимно погашаются, и относительная частота 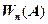 проявляет тенденцию к стабилизации, приближаясь к некоторой средней величине
проявляет тенденцию к стабилизации, приближаясь к некоторой средней величине 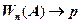 (при
(при 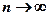 ).
).
Статистическая вероятность события –это относительная частота этого события, вычисленная по результатам большого числа испытаний.
Вероятность вычисляют до опыта, а относительную частоту – после опыта.
Для существования статистической вероятности события 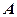 требуется:
требуется:
- возможность, хотя бы принципиально, производить неограниченное число испытаний, в каждом из которых событие 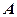 наступает или не наступает;
наступает или не наступает;
- устойчивость относительных частот появления 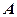 в различных сериях достаточно большого числа испытаний.
в различных сериях достаточно большого числа испытаний.
Недостатком статистического определения является неоднозначность статистической вероятности – зависимость от числа испытаний, от серии испытании и др.
Теорема Бернулли(Якоби Бернулли 1654-1705)–по мере неограниченного увеличения числа однородных и независимых испытаний относительная частота события 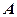 неограниченно приближается к некоторой постоянной величине: W → p;
неограниченно приближается к некоторой постоянной величине: W → p;
Число p , к которому приближается относительная частота события при неограниченно растущем числе экспериментов, называется статистическойвероятностью события 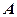 .
.
Не напоминая определения некоторых основных понятии (условная вероятность, сложение и умножение вероятностей, формула полной вероятности), отметим лишь, что полученные английским математиком Бейесом (опубликованы в 1764 г.) формулы позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие 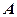 (т.е. априорные гипотезы апостериори переоцениваются):
(т.е. априорные гипотезы апостериори переоцениваются):
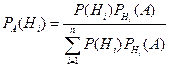 ,
,
где 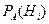 - вероятность гипотезы
- вероятность гипотезы 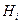 при условии, что появилось событие
при условии, что появилось событие 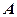 , а знаменатель – это
, а знаменатель – это 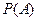 , т.е. полная вероятность события А.
, т.е. полная вероятность события А.
Формула Бернулли - биномиальное распределение (для однотипных повторяющийся независимых испытаниях – схема Бернулли) позволяет рассчитать вероятность появления события в 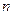 испытаниях ровно
испытаниях ровно 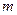 раз:
раз:
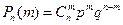 ; (2.1)
; (2.1)
где 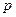 вероятность появления события в одном испытаний, а
вероятность появления события в одном испытаний, а 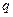 - не появления (
- не появления ( 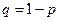 ),
), 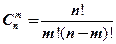 является одним из основных понятии раздела математики – комбинаторики и есть количество сочетании
является одним из основных понятии раздела математики – комбинаторики и есть количество сочетании 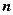 элементов по
элементов по 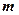 .
.
Биномиальный закон распределениядискретной СВ Х имеет место, если СВ принимает значения 0,1,2, … , m, … , n с вероятностями
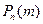 =
= 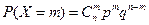 (формула Бернулли), (2.2)
(формула Бернулли), (2.2)
где 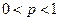 ,
, 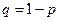 ,
, 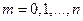 .
.
Это закон распределения числа Х=m появления события А в 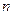 независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью
независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью 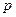 .
.
Закон называется «биномиальным» потому, что 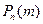 есть член разложения бинома Ньютона:
есть член разложения бинома Ньютона:
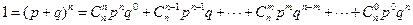 (2.3)
(2.3)
При большом числе испытаний воспользоваться формулой Бернулли практически невозможно, поэтому необходима была более простая (для вычислений) хотя и менее точная оценка вероятностей. Эта проблема была решена Муавром и Лапласом (Пьер Симон Лаплас – франц. астроном, математик и физик. 1749-1827)
Локальная теорема Лапласа – (для частного случая формула выведена Муавром в 1730г., а для общего случая – Лапласом в 1783 г.) Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля ( и больше чем 0,1) и единицы, то вероятность 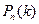 того, что событие А появится в n испытаниях ровно краз приближенно равна (тем точнее, чем больше n) значению функции
того, что событие А появится в n испытаниях ровно краз приближенно равна (тем точнее, чем больше n) значению функции
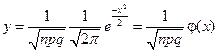 , при
, при 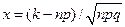 . (2.4)
. (2.4)
Так как функция 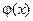 четная, то только для положительных значений аргумента
четная, то только для положительных значений аргумента 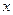 имеются таблицы значений этой функций (см. Прилож.1). Итак,
имеются таблицы значений этой функций (см. Прилож.1). Итак,
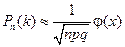 , (2.5)
, (2.5)
Формула Лапласа дает достаточно хорошие приближения лишь при достаточно больших значениях n.
Интегральная теорема Лапласа – производится n испытаний, в каждом из которых вероятность появления события А постоянна и равна р. Вероятность 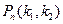 того, что А появится в n испытаниях не менее
того, что А появится в n испытаниях не менее  и не более
и не более 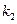 раз приближенно равна определенному интегралу
раз приближенно равна определенному интегралу
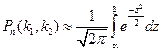 , (2.6)
, (2.6)
где 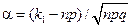 и
и 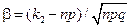 . (2.7)
. (2.7)
Напоминая функцию Лапласа 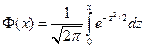 , (2.8)
, (2.8)
для значении которой имеются таблицы (см. П 2), перепишем формулу так:
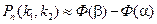 (2.9)
(2.9)
Распределение Пуассона – закон распределения вероятностей массовых (n велико) и редких (р мало) событий. Важное допущение: произведение числа испытаний n и вероятности р сохраняет постоянное значение: 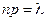 . Это означает, что среднее число появлений события в различных сериях испытаний (т.е. при различных значениях n) остается неизменным. Вероятность появления интересующего нас события в серии n испытаний ровно
. Это означает, что среднее число появлений события в различных сериях испытаний (т.е. при различных значениях n) остается неизменным. Вероятность появления интересующего нас события в серии n испытаний ровно 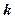 раз начинаем вычислить по формуле Бернулли. При предельном переходе
раз начинаем вычислить по формуле Бернулли. При предельном переходе 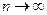 (следовательно
(следовательно 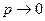 ) получаем формулу Пуассона:
) получаем формулу Пуассона:
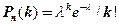 (2.10)
(2.10)
Знак приближенного равенства отпущен для простоты записи.
Формула Пуассона считается математической моделью простейшего потока событий.
Оказывается, что достаточно большое число однородных случайных событий независимо от их конкретной природы подчиняются определенным закономерностям, а именно вероятностным закономерностям.
Предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий.
На теорию вероятностей опирается математическая статистика, задача которой рассчитать оценки характеристик случайной величины (СВ) по имеющимся ее ограниченным данным наблюдения (выборке) и восстановить с определенной степенью достоверности характеристики (давать интервальные оценки истинных значений характеристик с определенной степенью надежности), присущие всему мыслимому набору значении СВ (генеральной совокупности).
Первое основное понятие математической статистики случайная величина:
-это числовая функция, определенная на пространстве элементарных событий
(на множестве элементарных исходов);
-это величина, которой мы не можем приписать определенное значение, но можем приписать несколько значений (или область значений), которые она принимает с определенными вероятностями;
- это величина, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.
Случайные величины встречаются нам повсюду: курс доллара или температура воздуха в наугад взятый день, цены товаров, время ожидания транспорта, количество посетителей в парикмахерскую или количество звонков в диспетчерскую за конкретный интервал временны, число родившихся мальчиков среди ста новорожденных, количество очков попадании в серии выстрелов и т.п.
Различают дискретныеинепрерывные СВ. Дискретнойназывают такую СВ, которая принимает конкретные (отдельные, изолированные, точечные) счетное число значения с определенными вероятностями. Непрерывнойназывают такую СВ, которая может принимать любое значение из некоторого конечного или бесконечного числового промежутка (интервала). Например, дальность полета снаряда, время (момент) звонка на диспетчерскую скорой помощи, температура воздуха в определенный момент временны и т.д.. Большинство СВ, рассматриваемых в экономике, имеют настолько большое число возможных значений (например, число пассажиров в аэропорту, покупателей в магазине, зрителей на стадионе и т.п.), что их удобнее представлять в виде непрерывных СВ.
Наиболее полным, исчерпывающим описанием СВ является ее закон (ряд) распределения:всякое соотношение(функция), устанавливающее связь между возможными значениями СВ и соответствующими им вероятностями (их возможного появления).
Для дискретной СВ закон распределения может быть задан в виде таблицы, аналитически и графически. Возможные (т.е. могут наблюдаться на исходе ) значения СВ принято записывать в таблице строго по порядку возрастания. Например,
Таблица 2.1
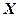
| 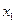
| 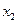
| … | 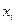
| … | 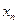
|
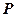
| 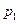
| 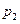
| … | 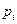
| … | 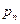
|
Для любой дискретной СВ 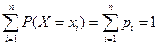 , (2.11)
, (2.11)
так как в результате испытания обязательно (достоверно) появится то или иное (одно и только одно) значение СВ из всевозможных значении.
Если по оси абсцисс откладывать значения СВ, по оси ординат – соответствующие их вероятности, то получаемая (соединением точек) ломаная называется полигоном распределения вероятностей.
Важными числовыми характеристиками (числа, которые описывают СВ суммарно) СВ являются математическое ожиданиеи дисперсия.
Математическим ожиданием дискретной СВ называют сумму произведений всех ее возможных значений на их вероятности:
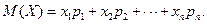 (2.12)
(2.12)
Если дискретная СВ Х принимает счетное множество значений, то
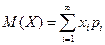 , (2.13)
, (2.13)
причем, мат. ожидание существует, если ряд в правой части (т.е сумма) абсолютно сходится. Мат. ожидание приближенно равно среднему значению 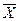 СВ (тем точнее, чем больше число испытаний): при решений многих задач, не зная соответствующие вероятности появления значений СВ, вероятности берут равными (при большом числе значений СВ их считают приблизительно равновозможными). Для решения многих задач достаточно знать лишь мат. ожидание. Например, если известно, что мат. ожидание числа выбиваемых очков у первого стрелка больше, чем у второго, то первый стрелок в среднем выбивает больше очков, чем второй, и, следовательно, стреляет лучше второго.
СВ (тем точнее, чем больше число испытаний): при решений многих задач, не зная соответствующие вероятности появления значений СВ, вероятности берут равными (при большом числе значений СВ их считают приблизительно равновозможными). Для решения многих задач достаточно знать лишь мат. ожидание. Например, если известно, что мат. ожидание числа выбиваемых очков у первого стрелка больше, чем у второго, то первый стрелок в среднем выбивает больше очков, чем второй, и, следовательно, стреляет лучше второго.
Свойства мат.ожидании:
1. 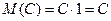 мат. ожидание постоянной величины есть само постоянное,
мат. ожидание постоянной величины есть само постоянное,
2. 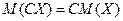 постоянный множитель выносится за знак мат. ожидания,
постоянный множитель выносится за знак мат. ожидания,
3. 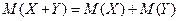 , (верно и для нескольких СВ)
, (верно и для нескольких СВ)
4. 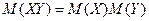 мат. ожидание произведения двух независимых СВ равно произведению их мат. ожиданий (верно и для нескольких взаимно независимых СВ).
мат. ожидание произведения двух независимых СВ равно произведению их мат. ожиданий (верно и для нескольких взаимно независимых СВ).
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна 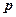 . Биномиальная СВ Х это число появлении А в серии
. Биномиальная СВ Х это число появлении А в серии 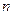 независимых испытании. Тогда мат. ожидание (приблизительно среднее число) числа появлений события А в серии этих испытаний равно:
независимых испытании. Тогда мат. ожидание (приблизительно среднее число) числа появлений события А в серии этих испытаний равно:
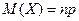 (2.14)
(2.14)
Доказательство. Число 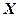 появления события
появления события 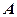 в
в 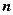 независимых испытаниях складывается из числа появлений события в отдельных испытаниях:
независимых испытаниях складывается из числа появлений события в отдельных испытаниях: 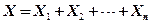 , где
, где 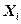 - число появлений события в
- число появлений события в 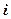 -ом испытании. По третьему свойству иммем:
-ом испытании. По третьему свойству иммем: 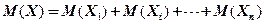 ,
,
где каждое слагаемое есть мат. ожидание числа появлений события в одном испытании и, следовательно, равно вероятности события 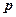 . Складывая, получаем (2.14).
. Складывая, получаем (2.14).
Дисперсия (рассеяние, разброс) дискретнойСВ.
Случайные величины могут иметь одинаковые мат. ожидания, но различные множества возможных принимаемых значений. Поэтому, для того чтобы оценить, как рассеяны возможные значения СВ вокруг ее мат. ожидания, вводят вторую важную числовую характеристику – дисперсию.
Может показаться, что для оценки меры рассеянности проще всего вычислить все возможные значения отклонения СВ от ее мат. ожидания ( 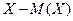 ) и затем найти их среднее значение, т.е.
) и затем найти их среднее значение, т.е. 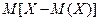 . Однако одни возможные отклонения положительны, а другие – отрицательны; в результате их взаимного погашения среднее значение отклонения равно нулю. Т.е. в итоге простого сложения отклонении мы теряем меру разбросанности СВ, поэтому целесообразно заменить возможные отклонения их абсолютными значениями или их квадратами. Но оперировать с абсолютными величинами затруднительно, поэтому вычисляют среднее значение квадрата отклонения, которое и называют дисперсией:
. Однако одни возможные отклонения положительны, а другие – отрицательны; в результате их взаимного погашения среднее значение отклонения равно нулю. Т.е. в итоге простого сложения отклонении мы теряем меру разбросанности СВ, поэтому целесообразно заменить возможные отклонения их абсолютными значениями или их квадратами. Но оперировать с абсолютными величинами затруднительно, поэтому вычисляют среднее значение квадрата отклонения, которое и называют дисперсией:
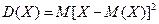 . (2.15)
. (2.15)
Пользуясь свойствами мат. ожидания, можно получить формулу:
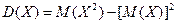 (2.16)
(2.16)
Свойства дисперсии:
1. 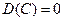 , дисперсия постоянной величины равна нулю.
, дисперсия постоянной величины равна нулю.
2. 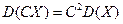 ,
,
3. 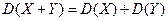 , дисперсия суммы двух независимых СВ равна сумме дисперсий этих случайных величин (верно и для нескольких взаимно независимых СВ).
, дисперсия суммы двух независимых СВ равна сумме дисперсий этих случайных величин (верно и для нескольких взаимно независимых СВ).
4. 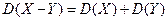 .
.
Если 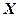 и
и 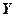 независимые СВ, то
независимые СВ, то
5. 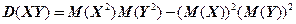 .
.
Пусть производится 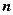 независимых испытаний, в каждом из которых вероятность появления события
независимых испытаний, в каждом из которых вероятность появления события 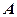 постоянна и равна
постоянна и равна 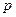 (схема Бернулли). Тогда дисперсия числа появлений события
(схема Бернулли). Тогда дисперсия числа появлений события 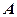 вычисляют по формуле:
вычисляют по формуле:
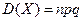 . (2.17)
. (2.17)
Доказательство. Как и для мат. ожидания здесь аналогично получим (по третьему своиству) 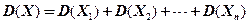 , где каждое слагаемое по формуле есть
, где каждое слагаемое по формуле есть 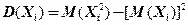 . Учитывая, что
. Учитывая, что 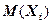 =
= 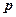 и то, что
и то, что 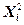 принимает значение
принимает значение 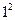 с вероятностью
с вероятностью 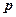 и
и 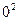 с вероятностью
с вероятностью 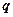 , т.е.
, т.е. 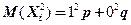 =
= 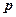 , получим
, получим 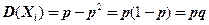 .
.
Следовательно, 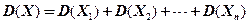 =
= 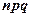 .
.
Средним квадратическим отклонениемСВ Х называют корень из дисперсии:
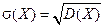 (2.18)
(2.18)
Чтобы оценить дисперсию (разброс) значений СВ в процентах относительно ее среднего значения, вводится коэффициент вариации - 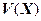 , рассчитываемый по формуле
, рассчитываемый по формуле
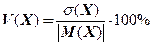 .
. 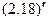
Теорема. Среднее квадратическое отклонение суммы конечного числа взаимно независимых СВ равно:
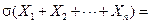
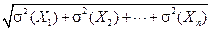 (2.19)
(2.19)
Для одинаково распределенных взаимно независимых СВ (которые, следовательно, имеют одинаковые числовые характеристики, пусть, например, мат. ожидание всех равно 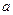 ), обозначим среднее арифметическое через
), обозначим среднее арифметическое через
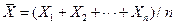 (2.20)
(2.20)
Тогда имеет место три положения:
1. 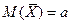 ; 2.
; 2. 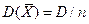 ; 3.
; 3. 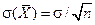 ;
;
Докажем, например, второе положение: дисперсия среднего арифметического 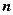 одинаково распределенных взаимно независимых СВ в
одинаково распределенных взаимно независимых СВ в 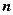 раз меньше дисперсии каждого из СВ
раз меньше дисперсии каждого из СВ
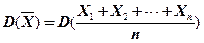 =
= 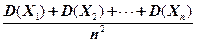 = =
= = 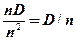 . (2.20’)
. (2.20’)
Математическое ожидание пуассоновской СВ 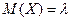 , (
, ( 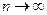 ,
, 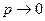 ,
, 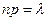 ).
).
Дисперсия пуассоновской СВ  , (
, ( 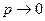 ,
, 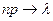 ,
, 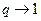 ,
, 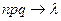 ).
).
Непрерывные случайные величины. Функция распределения (вероятностей).
Ряд распределения для непрерывной СВ построить нельзя, поэтому пользуются не вероятностью события 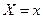 , а вероятностью события
, а вероятностью события 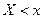 , где
, где 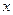 - текущая переменная.
- текущая переменная.
Функцией распределенияСВ 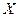 называется функция F(x), выражающая вероятность того, что СВ примет значение, меньшее
называется функция F(x), выражающая вероятность того, что СВ примет значение, меньшее 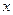 :
:
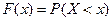 . (2.21)
. (2.21)
Из определения следуют свойства:
1) 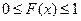 ; 2)
; 2) 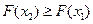 , при
, при 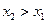 ;
;
3) 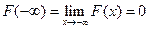 и
и 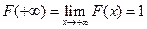 ;
;
4) 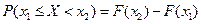 , т.е. (2.22)
, т.е. (2.22)
вероятность попадания СВ в интервал 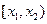 равна приращению ее функции распределения на этом интервале. При неограниченном уменьшении интервала получим: вероятность того, что СВ примет отдельно взятое (точечное) значение, которое равно:
равна приращению ее функции распределения на этом интервале. При неограниченном уменьшении интервала получим: вероятность того, что СВ примет отдельно взятое (точечное) значение, которое равно:
- нулю, если функция распределения вероятностей СВ непрерывна,
- величине разрыва, если функция терпит разрыв в этой точке.
Плотностью распределения (вероятностей)непрерывной СВ Х называют первую производную от функции распределения: 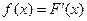 , (обозначают также через
, (обозначают также через 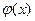 ).
).
Теорема:Вероятность попадания непрерывной СВ в заданный интервал (a,b) равна :
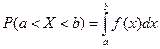 ,
,
(геометрический - это площадь под графиком 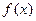 ).
).
Встречаются и другие названия плотности распределения – плотность вероятностей, дифференциальная функция распределения, дифференциальный закон распределения.
Свойства плотности распределения:
1. 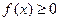 ,
,
2. 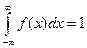 , геометрически это означает, что вся площадь ограниченной графиком функции и осью ОХ, равна единице. В вероятностном смысле это означает, что СВ на исходе испытания (наблюдения) обязательно примет какое-либо конкретное значение.
, геометрически это означает, что вся площадь ограниченной графиком функции и осью ОХ, равна единице. В вероятностном смысле это означает, что СВ на исходе испытания (наблюдения) обязательно примет какое-либо конкретное значение.
3. Вероятность попадания непрерывной СВ в интервал 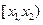 равна :
равна :
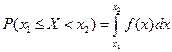 (2.23)
(2.23)
4. Функция распределения непрерывной СВ выражается через плотность вероятности по формуле:
5. 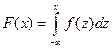 . (2.24)
. (2.24)
Числовые характеристики непрерывной случайной величины (СВ):
- Математическое ожиданиенепрерывной СВ –
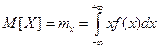 ; (2.25)
; (2.25)
- Мода (М) –(обозначают также МоХ и 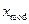 ) это тозначение СВ, которое имеет максимальную вероятность (при котором функция плотности вероятностей достигает максимума),
) это тозначение СВ, которое имеет максимальную вероятность (при котором функция плотности вероятностей достигает максимума),
- Медиана (Ме) –этото значение СВ, при которой 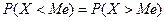 , т.е. медиана делит всю вероятность на две равные части. Графический, для непрерывной СВ, означает площади под графиком
, т.е. медиана делит всю вероятность на две равные части. Графический, для непрерывной СВ, означает площади под графиком 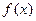 слева и справа от Ме равны.
слева и справа от Ме равны.
- Квартили -это такие границы - 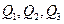 которые делят всю вероятность на четыре равные части. Разность правой и левой квартилей
которые делят всю вероятность на четыре равные части. Разность правой и левой квартилей 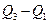 может быть использована как показатель вариации.
может быть использована как показатель вариации.
Дата добавления: 2016-09-20; просмотров: 3262;
