Распределение (хи-квадрат) – распределение Пирсона

Распределение 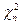с n степенями свободы называется распределение суммы квадратов n независимых СВ, распределенных по стандартному нормальному закону:

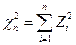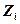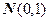, где ~ . (2.41)

Число степеней свободы функций 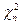(т.е. число 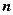) определяется числом ее составляющих СВ, минус число линейных связей между ними. Например, если 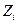связаны одним линейным соотношением 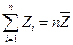, то число степеней свободы рано .

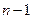Плотность этого распределения при 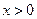равен

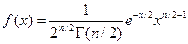, и равен нулю при 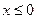(2.42)

где 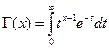- гамма-функция; в частности, .

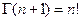Из определения следует, что распределение «хи квадрат» зависит из одного параметра – числа степеней свободы. При 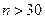распределение СВ 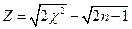близко к стандартному нормальному 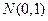. Поэтому обычно таблицы задаются для .

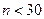График плотности вероятностей СВ, имеющей 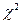распределение, имеет асимметричный вид (рис. 2.4), однако с увеличением числа степеней свободы распределение «хи-квадрат» постепенно приближается к нормальному.

Числовые характеристики:

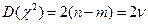, , (2.43)

где 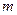- число связей между 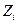, а 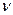- число степеней свободы СВ, распределенной по «хи квадрату».

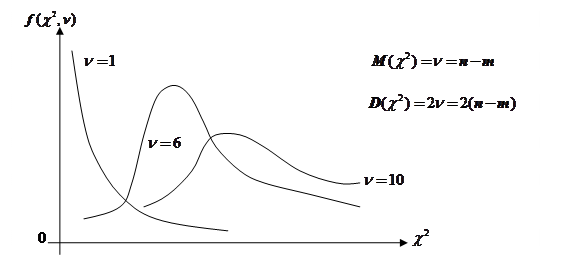
Рис. 2.4

Есл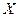и и 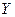- две независимые 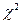- распределенные СВ со степенями свободы 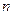и 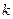соответственно ( 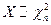, ), то их сумма 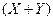также 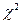-распределенная СВ с числом степеней свободы 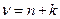. Распределение 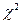(ее критические границы) применяется при построении доверительных интервалов и проверке гипотез.