Биномиальное распределение
В системах ЭСН для нормального функционирования, повышения надежности эксплуатации и создания оптимального резерва стремятся по возможности использовать однотипное оборудование (выключатели, трансформаторы, привода и т. п.). Это оборудование может находиться в исключающем друг друга состояниях (исправно или неисправно, включено или выключено и т. д.).
Произведем nнезависимых опытов, в каждом из которых может появиться или не появиться некоторое событие А (например, выключатель включен). Вероятность появления события А в каждом опыте равна p, а вероятность непоявления q = 1 — р. Требуется найти вероятность рnm того, что событие А в этих nопытах появится ровно mраз. [5]
Рассмотрим сложное событие Вm, состоящее в том, что событие А появится в nопытах ровно mраз. Это событие может осуществиться различными способами. Представим событие Вmкак сумму произведений событий, состоящих в появлении или непоявлении события А в отдельном опыте.
Будем обозначать Аi появление события А в i-ом опыте; Āi — непоявление события А в i-ом опыте.
Очевидно, каждый вариант появления события Вm (каждый член суммы) должен состоять из mпоявлений события A и п-т непоявлений, т. е. из mсобытий A и п-т событий Ā с различными индексами:
Bm = A1A2…Am 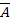 m+1…
m+1… 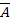 n +…+ A1
n +…+ A1 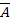 2 A3…
2 A3…
… 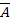 n-1 An+…+
n-1 An+…+ 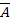 1
1 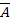 2…
2… 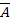 n-m An-m+1…An, (5.3)
n-m An-m+1…An, (5.3)
Причем в этом выражении в каждое произведение событие А должно входить mраз, а Ā должно входить п-т раз.
Число всех комбинаций такого рода равно Сnm, т. е. числу способов, какими можно из nопытов выбрать m,в которых произошло событие A. Вероятность каждой такой комбинации, по теореме умножения для независимых событий, равна рmqn-m. Так как комбинации между собой несовместны, то, по теореме сложения, вероятность сложного события Вmбудет равна:
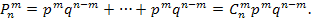 (5.4)
(5.4)
где Сnm — число слагаемых вида рmqn-m, равное числу комбинации.
Таким образом, если производится nнезависимых опытов, в каждом из которых событие А появится с вероятностью p, то вероятность того, что событие А появится ровно mраз выражается формулой:
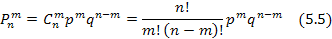
Формула (5.5) является аналитическим выражением биномиального закона распределения и носит название формулы Бернулли.
При биномиальном распределении начальный момент первого порядка обозначается математическим ожиданием: m1 = пр. Центральный момент второго порядка — дисперсия: μ2 = Д = прq.
Выделим некоторые частные вероятности, облегчающие решение практических задач:
— вероятность того, что все элементы выключены (повреждены):
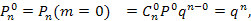 (5.6)
(5.6)
— вероятность того, что в рассматриваемой группе работают от m1 до m2 элементов:
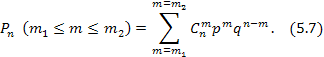
Дата добавления: 2016-05-25; просмотров: 1565;
