Метод минимальных путей и сечений

Метод базируется на представлении сетевых систем графом сети (граф С). К сетевым системам относятся физические системы, предназначенные для распределения электроэнергии, газа, воды, пара и пр. Геометрическое изображение сети может быть представлено графом, у которого направление дуг необязательно должно совпадать с направлением физического потока, поэтому граф является частично ориентированным. Условием ориентирования графа сети является расположение базисных узлов, относительно которых производится оценка надежности системы.

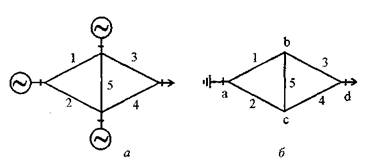
Рисунок 4.8 — Схема системы (а) и граф сети (б)

Реальная схема электрических соединений преобразуется в структурную (граф С), при этом последовательно и параллельно соединенные элементы заменяются эквивалентными. Элементам графа С присваиваются названия (обозначения) физической сети: вершинам — пункты присоединений, дугам — ЛЭП. Кроме этих вершин в графе образуются вершина ИП и так называемый узел земли, который получается в результате объединения всех нейтралей ИП.

Представление электрической схемы графом сети дает возможность упростить расчеты и применить для вычислений матрицу путей, по которым возможны связи между источником и нагрузкой. Из этих путей выделяются минимальные пути, состоящие из элементов, работоспособное состояние которых обеспечивает передачу электроэнергии от ИП к узлу нагрузки.

В этой матрице единица (1), стоящая на пересечении строки (путь П) и столбца (i), означает, что i-й элемент или узел входит в путь Пi; ноль (0) означает, что i-й элемент или узел не входит в путь Пi.

Из матрицы путей нетрудно получить матрицу сечений. Сечения при этом могут быть одноэлементными, двухэлементными и т.д.

Минимальными сечениями системы называются совокупности минимального набора элементов, одновременные отказы которых приводят к перерыву ЭСН узла нагрузки.

Если все пути содержат один элемент, то этот элемент является одноэлементным сечением (узлы а и d) и соответствует схеме одного отказа при оценке надежности системы.

Если пути содержат два одинаковых элемента, то эти элементы образуют двухэлементное сечение, что соответствует схеме двух отказов.

Вероятность отказа системы (рисунок 4.8) без учета преднамеренных отключений относительно узла нагрузки d имеет вид:

Q = qa + q1q2 + qbqc + q3q4 + q5q1q4 + q5q2q3 + qd (4.20)

При расчете показателей надежности с помощью структурных схем анализируются не все возможные состояния схемы, а только состояния безотказной работы того минимального набора элементов, которые обеспечивают нормальное функционирование схемы (передачу энергии) от ИП до узла нагрузки (минимальные пути) или отказ того минимального набора элементов, отказ которого в любом из наборов приводит к отказу системы относительно рассматриваемого узла (минимальные сечения).

С помощью минимальных путей или сечений, полученных в результате структурного анализа, можно определить вероятность обесточения узла нагрузки. Рассмотрим основные положения и определения теории графов, используемые в структурном анализе, целью которого является определение минимальных путей или минимальных сечений.[5]

Графом называются два любых множества А и В, в которых каждому элементу из множества А соответствуют два элемента из множества В. Элементы А и В называются соответственно ребрами и вершинами графа. Вершины, соответствующие ребру, называются концами ребра. Ребро называется ориентированным, если один из его концов рассматривается как начало, а другой как окончание. На схеме ориентированное ребро изображается как отрезок со стрелкой. Граф, в котором отдельные ребра ориентированы, называется частично-ориентированным. Граф, где все ребра ориентированы, называется ориентированным. Граф без ориентации ребер называется неориентированным.

Изучение структуры той или иной схемы равносильно изучению структуры графов. Граф называется планарным, если он может быть изображен на плоскости без пересечений ребер в точках, не являющихся вершинами графа, в противном случае граф является непланарным. Для системы ЭСН свойство планарности, как правило, выполняется, так как переходы линий друг над другом встречаются относительно редко.

Анализ связей при расчетах надежности заключается, прежде всего, в нахождении и оценке путей между его вершинами, т. е. ИП и узлами нагрузки. Путем графа называется такая последовательность ребер, в которой конец каждого предыдущего ребра совпадает с началом последующего. Однореберный путь называется непосредственным, многореберный — транзитным.

Существует много способов определения минимальных путей графа. Эти способы делятся на аналитические и логико-цифровые (последние реализуются обычно только на ЭВМ) и основаны на аналитическом представление схемы в виде матрицы непосредственных путей. По путям графа можно также определить и минимальные сечения. Чтобы составить структурную схему (граф сети), необходимо предварительно преобразовать схему электрической сети в расчетную схему надежности, т. е. схему функционирования сети. Последовательно соединенные элементы между двумя узлами целесообразно заменить одним эквивалентным, параметры которого определяются по известным формулам. Аналогичный прием применяется для элементов, параллельно включенных между двумя узлами.

После этого элементам расчетной схемы ставятся в соответствие ребра графа, а пунктам физического соединения (СШ, трехобмоточным трансформаторам, местам подключения ответвлений к магистральным линиям) — вершины графа. Надежность пунктов физического соединения элементов и коммутационной аппаратуры может учитываться введением в расчетную схему элементов соответственно логике функционирования их в электрической системе. Кроме указанных вершин в графе сети будет еще одна особая вершина — вершина источников, иногда называемая вершиной «истока». ИП, если вероятность его безотказной работы отличается от 1, вводится РЭ надежности. Все свободные концы ребер элементов таких ИП объединяются в вершину — «исток».

Обычно граф сети с учетом возможных направлений потоков мощности в элементах является частично-ориентированным. Направленность графа сети относительно разных узлов нагрузки может быть различной. Поэтому для оценки надежности системы относительно различных узлов нагрузки следует каждый раз проверять ориентировку ребер исходного графа. Построение и составление исходной схемы в виде графа дает возможность упростить процесс исследования надежности системы алгебраической методикой вычисления.

В качестве аналитического образа графа используется матрица непосредственных путей, которая строится следующим образом.

1 Нумеруются вершины исходного графа. Для удобства расчетов нумерацию рекомендуется начинать с вершины источников. Порядок матрицы равен числу вершин в исходном графе.

2 Строки и столбцы матрицы обозначаются номерами вершин графа.

3 Элементу, принадлежащему i-ой строке j-му столбцу матрицы A,присваивается некоторое число (единица или значение вероятности надежной работы элемента) если из вершины i к вершине jимеется непосредственный путь; если пути нет — ставится нуль.

Если указанному элементу присваивается значение 1, то такую матрицу называют матрицей смежности. В случае расчета надежности схем очень сложной конфигурации для уменьшения порядка матрицы путей целесообразно разделить схему на несколько частей.

Используя матрицу непосредственных путей Ав качестве аналитического образа расчетной схемы по надежности, можно определить минимальные пути и минимальные сечения в сложной схеме. Существует несколько методов определения минимальных путей и соответственно минимальных сечений, которые достаточно подробно описаны [16].

После определения минимальных путей и сечений исходная сложная расчетная схема по надежности заменяется эквивалентной относительно узла, последовательно-параллельной — в случае путей или параллельно- последовательной — в случае сечений.

Такая замена дает возможность использовать известные приемы расчета, в частности применить формулы для суммы вероятностей совместных событий — безотказной работы путей или событий отказа сечении. Но следует иметь в виду, что пути и сечения в общем случае являются зависимыми, так как в них могут входить одни и те же элементы. Эту зависимость необходимо учитывать при определении вероятности надежной работы нескольких путей или вероятности отказа нескольких сечений в формуле для суммы вероятности совместимых событий при условии, что каждый путь может пропустить всю необходимую мощность в узел нагрузки.

При определении каждой последующей условной вероятности следует учитывать вероятность безотказной работы (отказа) только тех элементов, которые еще не входили в предыдущие пути (сечения).[5]

Конечный результат — вычисление вероятности отказа системы относительно интересующего нас узла нагрузки или вероятность безотказной работы при представлении схемы в виде минимальных сечений — достигается быстрее и проще, чем методом минимальных путей, однако процесс определения сечений сам по себе более трудоемкий.

На существующем этапе развития и применения этих методов в электроэнергетике нецелесообразно противопоставлять один метод другому, т. к. для схем с протяженной структурой и малым числом поперечных связей определенные преимущества будет иметь метод путей, а для схем с концентрированной структурой и большим числом поперечных связей предпочтителен метод сечений.

Методы расчета показателей надежности сложных схем с использованием минимальных путей и сечений достаточно просто позволяют учесть преднамеренное отключение элементов. Так, при представлении исходной схемы в виде минимальных путей вероятность отказа Qcпсхемы относительно n-го узла нагрузки складывается из суммы вероятностей двух гипотез: отказов всех путей 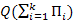и наложения на пред-намеренное отключение i-го элемента отказа оставшейся части схемы .

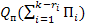Предполагаем, что преднамеренные отключения отдельных элементов не совмещаются:

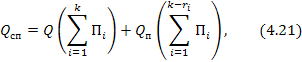
где 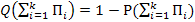, (4.22)

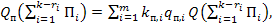(4.23)

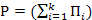— вероятность работы всех путей схемы, определяется по формуле для суммы вероятностей совместимых событий (4.80);

Qп i — вероятность преднамеренного отключения i-го элемента схемы;

ri — число путей, в которых содержится i-й элемент схемы;

(к — ri) — число путей, оставшихся после исключения i-го элемента из схемы;

kп i < 1 — коэффициент, учитывающий уменьшение вероятности отказов вследствие того, что возможно наложение аварии оставшейся части схемы на пред­намеренное отключение i-го элемента, а не наоборот;

т — число элементов в сложной схеме.

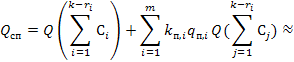
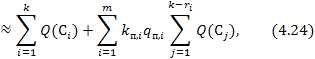
где(к — ri) — число сечений, оставшихся в схеме после исключения i-го элемента.

В оставшейся после исключения i-го элемента части схемы минимальные сечения получаются из сечений исходной полной схемы после исключения образовавшихся неминимальных сечений. Аналогичные приемы можно использовать для расчета надежности тех сложных схем, в которых возможны совмещения преднамеренных отключений различных элементов. В этом случае рассматриваются гипотезы наложения аварий на преднамеренные отключения двух и более элементов оставшихся частей схемы и гипотезы отказа схемы без учета преднамеренных отключений элементов.

Методы расчета показателей надежности сложных схем с использованием минимальных путей и сечений достаточно просто позволяют учесть преднамеренное отключение элементов.

Метод кратчайших путей и минимальных сечений нашел применение для оценки надежности сложных физических систем с несколькими тысячами элементов, в том числе и для энергосистем. Метод позволяет учитывать поперечные связи в схемах электрических соединений.