Метод расчетов надежности на основе графов цепей Маркова

Формирование моделей для расчета надежности систем и ЭЭУ производится с учетом реальных потоков событий, в результате которых происходит эволюция рассматриваемых объектов из состояния в состояние. Потоки событий возникают по причинам отказов, восстановлений, замены, плановых ремонтов элементов систем. Эволюция состояний описывается в виде траекторий переходов из одного состояния в другое с помощью цепей Маркова (рисунок 4.5).[14]

Рисунок 4.5 — Граф состояний ОРУ-220 кВ:

Р0 — вероятность нормального состояния;

Р1 — вероятность частично рабочего состояния;

Р2 — вероятность ремонтного состояния

Статическая модель системы при t→∞, соответствующая графу цепи Маркова (граф ЦМ), описывается линейными уравнениями вида:

где Рi, Рj — вероятности состояний, отн. ед.;

μji,ωij — интенсивность переходов, 1/год;

Gj — подмножество состояний Марковского процесса, из которых возможны переходы в i-e состояние (j Gj);

Gi — подмножество состояний, в которые возможны переходы из i-гo состояния (i Gi).

Для решения системы уравнений относительно Pi и Pj дополнительно вводится уравнение нормировки ΣРij = 1.

Схема ОРУ — 220 кВ, показанная на рисунке 4.2, может находиться в состояниях: нормального, когда все элементы находятся в работе; частично рабочего, при отказах отдельных элементов схемы на время устранения отказа, и ремонтного при плановом ремонте выключателей. Относительно РЭ блока 1 граф состояний (рисунок 4.5) описывается следующими линейными уравнениями:

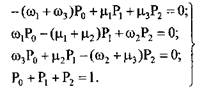
Входящие в эту систему уравнений интенсивности переходов рассчитываются по выражениям:

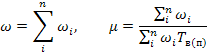
или (4.11)

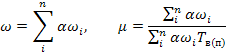
где n — количество элементов в системе;

Тв(п) — продолжительность восстановительных ремонтов или простоя, ч.

Применение представленного метода в целях оценки вероятности состояния схем электрических соединений или ЭЭУ ограничено в связи с большими вычислительными затратами, несмотря на более высокую точность по сравнению с другими методами.

Так, например, рассмотрим расчет количественных показателей при простейшем случае, когда объект имеет два состояния: работы и отказа, причём переходы из состояния в состояние происходят под воздействием пуассоновских потоков событий (нередко потоки принимаются стационарными).

Рисунок 4.6 — Состояния электросетевого объекта: S1 – объект исправен (работает), S2 – объект неисправен (находится в ремонте)

На объект, находящийся в состоянии S1, действует стационарный поток отказов с интенсивностью λ12, переводящий объект в состояние S2. На объект, находящийся в состоянии S2, действует стационарный поток восстановлений с интенсивностью μ21. Оба потока являются пуассоновскими и независимыми.

Вероятности нахождения объекта в состоянии работы – pраб и состоянии отказа – pотк в стационарном режиме определяются путем решения уравнений Колмогорова [4]:

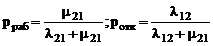. (4.12)

Исходя из свойств показательного распределения, среднее время нахождения объекта в работе составляет:

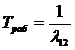, (4.13)

Среднее время нахождения объекта в состоянии отказа:

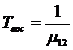. (4.14)

Подставляя (4.13) и (4.14) в (4.12), получим:

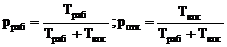. (4.15)

Последние выражения для вероятностей известны под названием соответственно коэффициент готовности (комплексный показатель надёжности) и коэффициент неготовности. Знаменатель в формулах (4.15) представляет собой среднее время между отказами (полный цикл «работа – отказ — восстановление»):

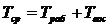. (4.16)

Подставляя (11) в (10) с учётом (6), получим:

или . (4.17)

Полученное выражение в [17] известно как фундаментальное уравнение, устанавливающее связь между тремя параметрами – показателями надёжности работы объекта.

Уравнение (4.17) с методической точки зрения интересно тем, что позволяет определить минимальное число показателей, которые дают достаточную оценку надёжности объекта. Исходя из (4.17), число таких показателей должно быть равно двум, а остальные, при необходимости, могут быть рассчитаны по формулам.