Метод расчетов структурно-функциональ-ной надежности электроэнергетических установок

Использование топологических структур графа Коутса (граф К) в качестве кинематических моделей для оценки надежности ЭЭУ расширяет диапазон исследований и позволяет решать задачи структурно-функциональной надежности [14]. Граф К соответствует системе линейных уравнений, записанных в общем виде: 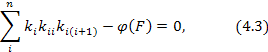где ki - совокупность вершин, отображающих переменные (i = 1,2, 3,...,n); kii, ki (i+1) - совокупность дуг, отображающих передачи; φ(F) - совокупности вероятностей внешних факторов воздействия. Аналитический способ преобразования графа К заключается в описании типовых графов К уравнениями относительно начального и конечного состояний системы и определения коэффициента готовности конечного состояния. Структурные схемы строятся для технологически связанных между собой элементов, которые образуют функциональные цепи. Функциональная цепь представляется направленным графом (рисунок 4.3), узлы которого соответствуют коэффициентом готовности функциональной цепи, а ветви - коэффициентам готовности элементов (ki, kj, kq). Вводятся понятия параметров начального к0 и конечного кn узлов. Узлы графа обладают собственными контурами (коо, кnn), к узлам отнесены действия факторов F, влияющих на изменение структурной схемы с вероятностью φ(F). Собственные контуры в узлах графа коо и knn характеризуют результат диагностического контроля работоспособного состояния отдельных или группы связанных элементов. Вероятность фактора F0 принимает дискретное значение 1 или 0 по результатам диагностического контроля. Целью расчета является определение коэффициента готовности конечного узла kn. 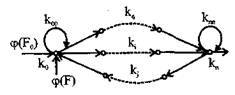Рисунок 4.3- Кинематическая модель надежности ЭЭУ Получены основные выражения kn для схем ЭЭУ, имеющих последовательно-параллельное соединение элементов с учетом действия стохастических факторов прямой и обратной связей. а) Коэффициент готовности кг кинематической системы при последовательном соединении элементов в смысле надежности согласно модели на рисунке 4.4 а) будет равен: 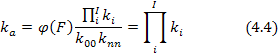где φ(F0) = 1; koo = knn = -1. б) При параллельно-последовательном соединении элементов в случае нагруженного резерва коэффициент готовности кинематической системы (рисунок 4.4 б))равен: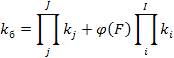 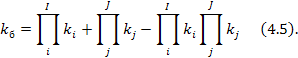Получена зависимость, соответствующая схеме с одной резервной функциональной цепью с элементами ki (или kj). При условии, что выполняется равенство: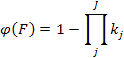 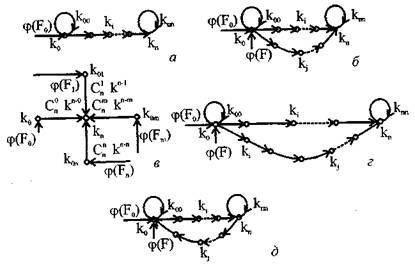Рисунок 4.4 - Кинематические модели систем: а - последовательное соединение элементов; б - параллельно-последовательное соединение элементов; в - система с кратным резервированием; г — последовательно-параллельное соединение элементов; д — система с обратной связью при действии защит в) В случаях, когда схемы имеют некоторую кратность резервирования (рисунок 4.4 в)), коэффициент готовности определяется по формуле биномиального распределения: 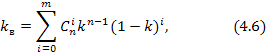где n- общее количество функциональных цепей, m — количество резервных цепей; 1 — k = φ(F) — вероятность отказа цепи или коэффициент простоя; к — коэффициент готовности однородной функциональной цепи. 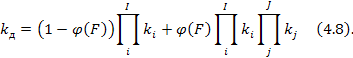г) Модель графа К, отображающая ненагруженный резерв (замещение), представляется в виде параллельно-последовательного соединения элементов с прямой стохастической связью (рисунок 4.4 б)): д) Включение параллельной функциональной цепи, состоящей из двух групп элементов, в случае изменения режима, например, регулирование нагрузки, под действием фактора с вероятностью φ(F) (рисунок 4.4 г)): е) Модель параллельно-последовательного соединения элементов с обратной стохастической связью, включающейся при действии фактора с вероятностью φ(F), например, при отключении ЭЭУ от защит (рисунок 4.4 д)):