Распределение Пуассона

Это распределение также как и биномиальное описывает характеристики дискретных СВ. [5]

Рассмотрим дискретную СВ X, которая может принимать только целые, неотрицательные значения: 0, 1, 2,...,m, причем последовательность этих значении теоретически не ограничена.

СВ X распределена по закону Пуассона, если вероятность того, что она примет определенное значение m,выражается формулой:

где а — некоторая положительная величина, называемая параметром закона Пуассона.

Последовательность вероятностей, задаваемая формулой (5.8), представляет собой ряд распределения, т. е. сумма всех вероятностей Рm равна единице и имеет вид:

Xm				…	m	…
Pm	e-a			…		…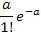

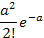
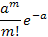
Зададим параметру а некоторые численные значения и определим вероятности Рm для различных значений т по формуле (5.8). В результате этих действии получим данные рядов распределения. На их основе построены многоугольники распределения СВ X, распределенной по закону Пуассона (рисунок 5.1).

Из рисунка 5.1 видно, что в зависимости от параметра а многоугольники распределения имеют существенные различия и по форме похожи на другие известные законы распределения СВ.

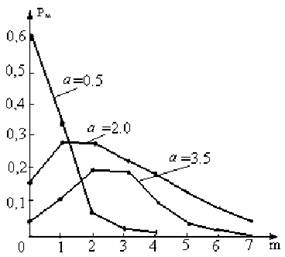
Рисунок 5.1 — Многоугольники распределения

Одной из основных числовых характеристик СВ X, распределенной по закону Пуассона, является математическое ожидание:

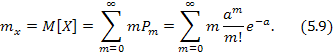
После некоторых преобразовании [3] получим: mx = а. Таким образом, параметр а представляет собой не что иное, как математическое ожидание СВ X.

Другая числовая характеристика – дисперсия, которая тоже равна параметру а, т. е. Дх = а.

Таким образом, дисперсия случайной величины, распределенной по закону Пуассона, равна ее математическому ожиданию а:

mx =Дх = a (5.10)

Это свойство распределения Пуассона часто применяется на практике для решения вопроса, правдоподобна ли гипотеза о том, что СВ X распределена по закону Пуассона. Для этого определяют из опыта статистические характеристики — математическое ожидание и дисперсию. Если их значения близки, то это может служить основанием в пользу гипотезы о пуассоновском распределении.

В задачах энергетики наибольший интерес представляют потоки событии, распределение которых описывается законом Пуассона.

Под потоком событийпонимается последова-тельность событий, происходящих одно за другим в какие-то моменты времени. Примерами могут служить: поток вызовов на телефонной станции; поток включений приборов в бытовой электросети; поток сбоев электронной вычислительной машины; потоки отказов энергетических объектов (выключателей, разъединителей, трансформаторов и др.) в достаточно большой системе и т. п.

События, образующие поток, в общем случае могут быть различными, но мы будем рассматривать лишь поток однородных событий, различающихся только моментами появления. Такой поток можно изобразить как последовательность точек t1, t2, ..., tkна числовой оси (рисунок 5.2).

Рисунок 5.2 — Представление потока событий

Рассмотрим на оси 0t простейший поток событий как неограниченную последовательность случайных точек (см. рисунок 5.2). Выделим произвольный участок времени длиной τ. Доказано [3], что при условиях стационарности, отсутствия последействия и ординарности потока событий, число точек, попадающих па участок τ, распределено по закону Пуассона с математическим ожиданием:

a = λτ, (5.11)

где λ — плотность потока (среднее число событий, приходящееся на единицу времени).

Вероятность того, что за время τ произойдет ровно m событий, будет равна:

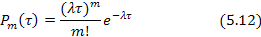
Вероятность того, что участок окажется пустым (не произойдет ни одного события):

Вероятность появления хотя бы одного события:

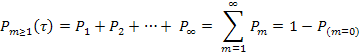
(5.14)

Вероятность того, что в интервале времени τ произойдет не менее к событии:

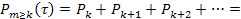
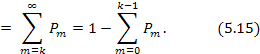
Важным свойством закона Пуассона является то, что он является предельным для биномиального распределения:

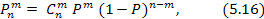
если одновременно устремлять число опытов п к бесконечности, а вероятность P – к нулю, причем их произведение пр сохраняет постоянное значение:

np = a (5.17)

Это предельное свойство биномиального распределения можно записать в виде:

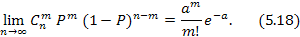
Предельное свойство биномиального закона часто находит применение на практике. Допустим, что производится большое количество независимых опытов п, в каждом из которых событие A имеет очень малую вероятность Р. Тогда для вычисления вероятности Рnm того, что событие А появится равно т раз, можно воспользоваться приближенной формулой:

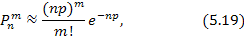
где пр = а — параметр закона Пуассона, которым приближенно заменяется биномиальное распределение.

От этого свойства закона Пуассона — выражать биномиальное распределение при большом числе опытов и малой вероятности события — происходит его название, часто применяемое в учебниках статистики: закон редких явлений.

Уместно заметить, что если при биномиальном распределении вероятностей (р + q)n, величины р и q не сильно отличаются друг от друга (не более чем на 2 порядка), например, p = 0,1 и = 0,9 или р = 0,5 и q = 0,5, то при увеличении числа опытов n→∞ асимптотой биномиального распределения будет нормальный закон распределения.

Если же р и q резко отличаются, т. е. p→0 или q→ 0, то при п→∞асимптотой биномиального распределения будет закон Пуассона (закон редких явлений).

Таким образом, биномиальное распределение сводится в пределе к двум — нормальному и пуассоновскому.