Выборочная ковариация и выборочный коэффициент корреляции

Наиболее употребляемыми характеристиками связи двух СВ являются меры их линейной связи – ковариация и коэффициент корреляции.

Выборочная ковариация является мерой взаимосвязанности двух переменных и позволяет выразить данную связь одним числом.

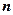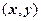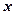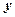При наличии выборки из наблюдений выборочная ковариация между и вычисляют по формуле:

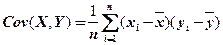(2.86)

Все свойства и правила ковариации, изложенные выше (см. 2.68 -2.70), имеют место и для выборочной ковариации.

Если теоретическая ковариация 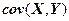не известна, то для ее оценки выборочную ковариацию 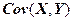умножают на 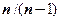(для «исправления» смещенности оценки).

.

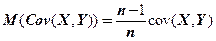Оценка теоретической ковариации имеет отрицательное смещение. Причина в том, что выборочные отклонения измеряются по отношению к выборочным средним значениям величин 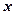и 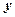и имеют тенденцию к занижению отклонений от истинных средних значений.

Итак, выборочная ковариация является смещенной оценкой теоретической ковариации, т. е. в большинстве случаев дает значения оценок, меньшие теоретических величин.

Выборочный коэффициент корреляции 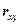определяется путем замены в формуле (2.69) теоретических дисперсии и ковариации на их несмещенные оценки:

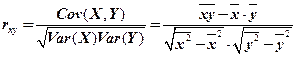, (2.87)

где 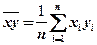, 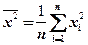. 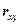является показателем тесноты связи и несмещенной оценкой теоретической корреляции 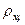. Отметим другие модификации формулы для выборочного коэффициента корреляции:

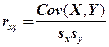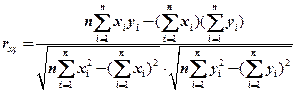; . (2.88)

Для практических расчетов наиболее удобна формула (2.87). Выборочный коэффициент корреляции 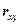(или просто 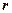), при достаточно большом объеме выборки, обладает те же свойствами что и 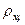(см. (2.69)).

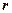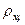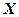Следует отметить, что является непосредственно оценкой генерального (теоретического) коэффициента корреляции между и 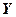лишь в случае двумерного нормального закона распределения СВ 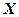и 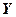. В других случаях (когда распределения 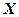и 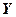отклоняются от нормального, например, одна из исследуемых величин - 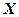не является случайной и т.п.) выборочный коэффициент корреляции не следует рассматривать как строгую меру взаимосвязи переменных.

Вопросы для самопроверки

1.Что такое генеральная совокупность и выборка?

2.Назовите основные виды выборок и способы отбора элементов в них.

3.Что такое статистический ряд и интервальный статистический ряд?

4.Дайте определение эмпирической функции распределения, приведите ее аналитическое и графическое представление.

5.Что такое полигон частот (относительных частот) и гистограмма? Для чего они используются?

6.Как вычисляются основные числовые характеристики по результатам наблюдения (выборки): выборочные среднее, дисперсия, среднее квадратическое отклонение?

7.Как вычисляется и где применяется выборочный коэффициент вариации?

8.Как вычисляются выборочная ковариация и выборочный коэффициент корреляции?

9.Приведите основные свойства выборочного коэффициента корреляции.