Определение. Число называется левосторонним пределом функции в точке , если: , так, что при выполняется: .

Обозначается .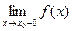

Односторонние пределы очень полезны при изучении функций, так как существуют такие ситуации, когда график функции слева и справа от некоторого 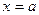стремится к разным ординатам.

Если односторонние пределы равны между собой, то существует предел функции в точке, если они разные, то предел не существует: ведь тогда 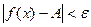для одной полуокрестности, но для второй полуокрестности эта разность не может быть меньше чем 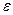, она будет .

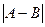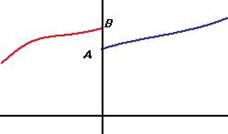
Представьте себе физический пример: температура 0 градусов. Если она понижается, проходя через 0, то есть до этого была положительна, то вода ещё не замёрзла, снега на улице нет. Если же она повышается и проходит через 0, например в марте, ситуация совсем иная - снег ещё не успел растяать. Как видно, ситуация при 0 градусов сильно зависит от того, какая температура была до этого.

Определение. Функция называется непрерывной в точке 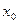, если в этой точке определено значение 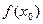, и оно совпадает как с правосторонним так и с левосторонним пределами:

.

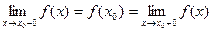Классификация:устранимый разрыв, разрыв 1 и 2 рода.

Устранимый разрыв.

Точка разрыва называется устранимой, если односторонние пределы равны 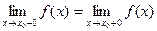причём равны конечному числу, но не существует 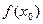или оно не равно пределу.

Пример. 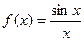. Формально 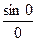вычислить нельзя, но предел есть, он раен 1. Получается график с одной выколотой точкой.

Пример. 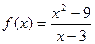. Точка 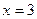- точка устранимого разыва. Значение не существует, но предел есть.

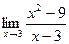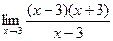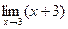= = = 6.

Можно доопределить значение функции в одной точке, то есть устранить разрыв. Поэтому он и называется устранимым.

Неустранимые разрывы делятся на 2 типа: