Доказательство формулы .
Запишем производную по определению.
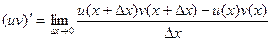
Но тут есть сдвиг на 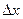 и по u, и по v. Добавим и вычтем такое слагаемое, в котором сдвиг по одной функции есть, а по второй нет:
и по u, и по v. Добавим и вычтем такое слагаемое, в котором сдвиг по одной функции есть, а по второй нет:
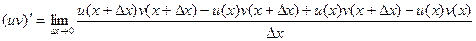 теперь слагаемых стало 4, но зато их можно сгруппировать по два, и даже разбить на две дроби, так, что дельта прибавляется только на одном из мест.
теперь слагаемых стало 4, но зато их можно сгруппировать по два, и даже разбить на две дроби, так, что дельта прибавляется только на одном из мест.
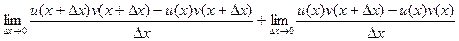
Теперь можно вынести тот множитель, который одинаков в каждой разности:
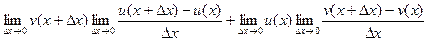
Видно, то, что осталось в дробях, это и есть производные для u или v соответственно, т.е. в итоге:
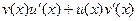 . Итак,
. Итак, 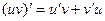 .
.
Докажем формулу .
Запишем по определению: 
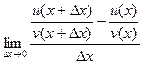 .
.
В том выражении, которое есть в числителе, приведём к общему знаменателю.
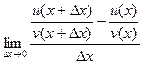 =
= 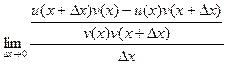 =
=
= 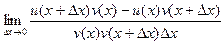 .
.
Аналогично как в прошлом случае, добавим и вычтем слагаемое, чтобы получилось 4 слагаемых а не два, и чтобы в каждой паре был сдвиг только по одной из функций. Можно для этой цели прибавить и отнять, например, 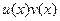 .
.
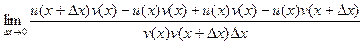 =
=
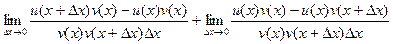
Если во втором пределе переставить два слагаемых и при этом, конечно, добавить знак минус, то часть, содержащая дельта-икс, получится раньше, что и приведёт к записи точь в точь, как в определении производной для v.
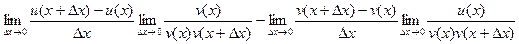 =
=
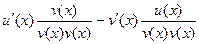 =
= 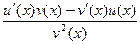 .
.
С помощью правил дифференцирования решим несколько примеров.
Пример.Найти производную тангенса (мы фактически докажем одну из формул таблицы интегралов).
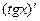 =
= 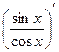 =
= 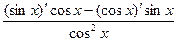 =
= 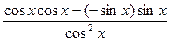 =
= 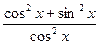 =
= 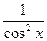 .
.
Итак, 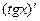 =
= 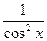 .
.
Пример. Найти 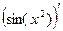 . Примерим формулу дифференцирования композиции.
. Примерим формулу дифференцирования композиции.
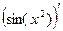 =
= 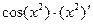 =
= 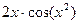 .
.
Дата добавления: 2016-12-26; просмотров: 787;
