Высказывания и операции над ними. Формулы

Высказыванием называется всякое утверждение, о котором можно вполне определенно и объективно сказать истинно оно или ложно.

Например, утверждение "2 > 0" является высказыванием и оно истинно, а утверждение "2 < 0" - ложно, утверждение "x² + y² = z²" высказыванием не является, так как оно может быть, как истинным, так и ложным при различных значениях переменных x, y, z. Высказывание полностью определяется своим истинностным значением. Условимся, значение истинности высказывания обозначать 1, если высказывание истинно, и 0, если высказывание ложно, что в точности соответствует значениям переменных булевых функций.

Различают высказывания простые и сложные, высказывание называется простым, если никакая его часть не является высказыванием. Простые высказывания будем обозначать начальными заглавными буквами латинского алфавита A, B, C или A₁, A₂, . . .. Сложные высказывания характеризуются тем, что образованы из нескольких простых высказываний с помощью логических операций, т.е. являются формулами алгебры высказываний.

Напомним, что алгебраической структурой или алгеброй называется структура, образованная некоторым множеством вместе с введенными на нём операциями. Определим алгебру высказываний.

Обозначим через B = {0, 1} – множество высказываний. Определим операции на множестве B.

Отрицанием высказывания A называется высказывание, которое принимает значение истина, если A ложно, и наоборот. Отрицание обозначается 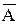(ØА) и является унарной операцией.

Пусть А и В - некоторые высказывания, введем бинарные операции над ними.

Конъюнкцией высказываний A и B называется высказывание, которое принимает значение истина тогда и только тогда, когда истинны оба высказывания A и B. Обозначается конъюнкция - A 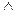B (А&В).

Дизъюнкцией высказываний A и B называется высказывание, которое принимает значение истина, если истинно хотя бы одно из высказываний A или B. Обозначается дизъюнкция - A 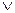B.

Импликацией высказываний A и B называется высказывание, которое принимает значение ложь тогда и только тогда, когда A истинно, а B ложно. Обозначается А®В.

Эквиваленцией высказываний A и B называется высказывание, которое принимает значение истина тогда и только тогда, когда высказывания A и B имеют одинаковые значения. Обозначение операции - А~В (АºВ).

Логические операции определяются, также, с помощью таблиц, называемых таблицами истинности. Приведем сводную таблицу истинности для всех введенных логических операций.

Пропозициональной (высказывательной) переменной называется переменная, значениями которой являются простые высказывания. Обозначим высказывательные переменные через X₁, X₂, . . . , X_n.

Понятие формулы алгебры высказываний вводится по индукции. Формулами алгебры высказываний являются:

1) логические константы 0 и 1;

2) пропозициональные переменные;

3) если АиВ –формулы, то каждое из выражений Ø(А), (А)Ù (В), (А)Ú (В), (А)® (В), (А) ~ (В) есть формула;

4) других формул, кроме построенных по пп. 1) - 3), нет.

Обозначим через M – множество всех формул алгебры высказываний, M является замкнутым относительно логических операций.

Для формулы построенной по п. 3 формулы Aи B называются подформулами. Число скобок в формуле можно сократить, Порядок выполнения операций в формуле определяется их приоритетом. Список логических операций в порядке убывания приоритета: 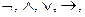~. Изменение порядка выполнения операций, как и в алгебраических операциях, производится с помощью круглых скобок.

Пусть U– формула над высказывательными переменными X₁, X₂, . . . , X_n, обозначается U(X₁, X₂, . . . , X_n). Набор конкретных значений высказывательных переменных X₁, X₂, . . . , X_n называется интерпретацией формулы Uи обозначаетсяI(U).

Формула называется выполнимой, если существует такой набор значений переменных, при которых эта формула принимает значение 1 (существует интерпритация I(U), на которой формула истинна).

Формула называется опровержимой, если существует такой набор значений переменных, при которых эта формула принимает значение 0 (существует интерпритация I(U), на которой формула ложна).

Формула называется тождественно истинной (ТИ-формулой) или тавтологией, если эта формула принимает значение 1 при всех наборах значений переменных (формула истинна на всех интерпретациях).

Формула называется тождественно ложной (ТЛ-формулой) или противоречием, если эта формула принимает значение 0 при всех наборах значений переменных (формула ложна на всех интерпретациях).

Формулы А и В называются эквивалентными (обозначается А º В), если при любых значениях высказывательных переменных значение формулы Асовпадает со значением формулы В.

Задачи определения эквивалентности, выполнимости, опровержимости, тождественной истинности и ложности формул могут решаться с помощью построения таблиц истинности, однако существуют менее громоздкие способы решения этих задач.