Полные системы операций. Алгебра Жегалкина
Система операций å называется полной, если любая логическая операция может быть представлена формулой над å.
Так как всякая формула может быть представлена приведенной формулой, то система å0 = {Ù, Ú, 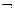 } - полна.
} - полна.
Система å сводится к å*, обозначается å®å*, если все операции системы å* представимы формулами над системой å. Если å* полна, то и å полна.
Последнее утверждение даёт один из способов доказательства полноты системы операций – сведение её к известной полной системе, например к å0. То есть полной будет система å, через операции которой можно выразить конъюнкцию, дизъюнкцию и отрицание.
Так в силу законов де Моргана, полными будут и системы å1 = {Ù , 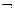 } и å2 = {Ú,
} и å2 = {Ú, 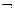 }.
}.
Алгебра над множеством логических функций с двумя операциями Ù и Å называется алгеброй Жегалкина. В алгебре Жегалкина выполняются следующие соотношения:
 ,
, 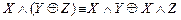 ,
,
 ,
, 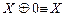 ,
,
а также ассоциативность, коммутативность, идемпотентность конъюнкции и свойства констант.
Задание. Доказать полноту системы å5 = {Ù, Å}.
Решение. Сведем систему å5 к полной системе å0.
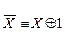
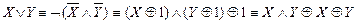 .
.
Если в произвольной формуле алгебры Жегалкина, реализующей булеву функцию f, раскрыть скобки и произвести все возможные упрощения, то получится формула, имеющая вид суммы произведений, то есть полинома по mod 2. Такая формула называется полиномом Жегалкина для данной функции. Линейной называется функция, полином Жегалкина которой линеен.
Сводимость к полной системе операций является необходимым условием полноты системы операций. Необходимое и достаточное условие полноты системы операций формулируется в терминах булевых функций.
Система булевых функций F называется полной, если любая функция может быть реализована формулой над F.
Замыканием множества F (обозначается [F]) называется множество всех булевых функций, реализуемых формулами над F. Класс функций называется замкнутым, если [F] = F.
Примеры замкнутых классов.
1. Класс функций, сохраняющих 0.
 .
.
2. Класс функций, сохраняющих 1.
 .
.
3. Класс самодвойственных функций.
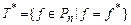 .
.
4. Класс монотонных функций.
 , где
, где
 .
.
5. Класс линейных функций.
 .
.
Принадлежность некоторых функций этим классам оформим в виде таблицы.
| Функция | Принадлежность классу | ||||
| T0 | T1 | T* | T£ | TL | |
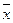
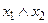
| + - - + | - + - + | - - + - | + + - + | + + + - |
Замкнутые классы попарно различны, не пусты и не совпадают с  .
.
Теорема 6.1 (Поста). Система булевых функций полна тогда и только тогда, когда она содержит хотя бы одну функцию, не сохраняющую 0, хотя бы одну функцию, не сохраняющую 1, хотя бы одну несамодвойственную функцию, хотя бы одну немонотонную функцию и хотя бы одну нелинейную функцию.
Доказательство.
Необходимость. Предположим противное, т.е. система булевых функций F полна ( [F] = 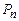 ) и входит в один из замкнутых классов ( F
) и входит в один из замкнутых классов ( F  Ú F
Ú F  Ú Ú F
Ú Ú F 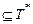 Ú F
Ú F 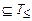 Ú F
Ú F  ). Обозначим через Ti тот класс, для которого справедливо включение F
). Обозначим через Ti тот класс, для которого справедливо включение F  . Тогда [F] =
. Тогда [F] = 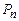
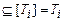 , что противоречит тому, что ни один из классов не совпадает с
, что противоречит тому, что ни один из классов не совпадает с  .
.
Достаточность. Пусть система булевых функций F содержит хотя бы по одной функции, не принадлежащих каждому из замкнутых классов. Т.е. $ F¢ =  , причем функции не обязательно различны и не обязательно исчерпывают F. Покажем, что отрицание и конъюнкция, которые образуют полную систему булевых функций, реализуются формулами над F¢.
, причем функции не обязательно различны и не обязательно исчерпывают F. Покажем, что отрицание и конъюнкция, которые образуют полную систему булевых функций, реализуются формулами над F¢.
1) Проведем вначале построение вспомогательных формул над F¢. Реализуем константы 0 и 1, которые будут использоваться в формуле для конъюнкции.
Для реализации 1 воспользуемся функцией 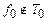 . Обозначим
. Обозначим 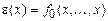 . Так как
. Так как 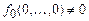 , то
, то  . Если
. Если  , то возможны 2 случая:
, то возможны 2 случая:
a)  и тогда
и тогда  реализует 1;
реализует 1;
b)  . В этом случае
. В этом случае  реализует отрицание, для построения формулы 1 воспользуемся функцией
реализует отрицание, для построения формулы 1 воспользуемся функцией 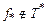 . Так как она несамосопряженная, то существует набор
. Так как она несамосопряженная, то существует набор  , на котором значение функции отличается от значения двойственной функции
, на котором значение функции отличается от значения двойственной функции 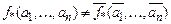 , тогда
, тогда 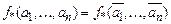 . Рассмотрим функцию
. Рассмотрим функцию  , для которой
, для которой 
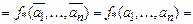
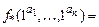
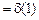 . Следовательно,
. Следовательно,  является константой, если
является константой, если 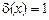 , то она реализует 1, если
, то она реализует 1, если 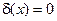 , то реализацией 1 будет функция
, то реализацией 1 будет функция 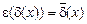 .
.
Константа 0 строится аналогично с использованием функции 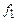 .
.
2) Для построения формулы, реализующей функцию отрицания, воспользуемся немонотонной функцией 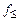 . Так как
. Так как  , то
, то 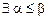 , такие что
, такие что 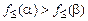 . Неравенство
. Неравенство 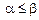 означает, что либо соответствующие координаты векторов
означает, что либо соответствующие координаты векторов 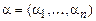 ,
,  совпадают, либо
совпадают, либо  и
и 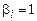 . Так как
. Так как 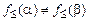 , то
, то  , а, следовательно, найдутся такие индексы, что
, а, следовательно, найдутся такие индексы, что  . Обозначим через I множество таких индексов. Определим функцию
. Обозначим через I множество таких индексов. Определим функцию  , где
, где  , если
, если 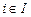 , и
, и  , если
, если 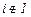 . Вычислим значение функции
. Вычислим значение функции 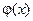 в 0 и 1:
в 0 и 1: 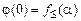 ,
,  . Так как
. Так как 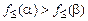 , то
, то  , а это означает, что
, а это означает, что 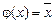 .
.
3) Для построения формулы, реализующей конъюнкцию, будем использовать нелинейную функцию 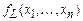 . Так как
. Так как 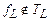 , то её полином Жегалкина содержит слагаемое, являющееся конъюнкцией, по крайней мере, двух переменных. Выберем произвольное слагаемое, содержащее наименьшее число переменных пусть это
, то её полином Жегалкина содержит слагаемое, являющееся конъюнкцией, по крайней мере, двух переменных. Выберем произвольное слагаемое, содержащее наименьшее число переменных пусть это 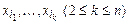 . Рассмотрим функцию, полученную заменой всех переменных, не вошедших в этот набор, нулями, т.е.
. Рассмотрим функцию, полученную заменой всех переменных, не вошедших в этот набор, нулями, т.е.  . Её полином Жегалкина имеет вид
. Её полином Жегалкина имеет вид
 . Рассмотрим функцию
. Рассмотрим функцию
 , где
, где  ,
, 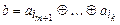 ,
, 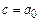 . Определим функцию
. Определим функцию
 ,
,
Такое представление корректно, так как  являются константами 0 или 1, определенными ранее формулами над F¢, а сложение по модулю 2 с константой дает либо функцию, либо её отрицание, которое также выражено формулой над F¢. Преобразуем
являются константами 0 или 1, определенными ранее формулами над F¢, а сложение по модулю 2 с константой дает либо функцию, либо её отрицание, которое также выражено формулой над F¢. Преобразуем 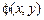 , воспользовавшись представлением c,
, воспользовавшись представлением c,

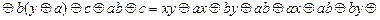
 . Таким образом, функция
. Таким образом, функция  реализует конъюнкцию.
реализует конъюнкцию.
Выводимость
Пусть задано множество формул от высказывательных переменных 
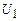 (
( 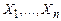 ),
), 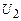 (
( 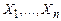 ), . . . ,
), . . . , 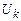 (
( 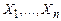 ). (1)
). (1)
Это множество формул назовем системой посылок.
Определение.Формула 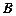 (
( 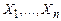 ) называется выводимой из системы формул (1) в алгебре высказываний, что обозначается
) называется выводимой из системы формул (1) в алгебре высказываний, что обозначается 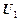 , . . ,
, . . ,  ú-
ú- 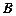
 , тогда и только тогда, когда формула
, тогда и только тогда, когда формула
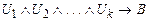 (2)
(2)
является ТИ-высказыванием, т.е. ú= 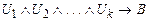 .
.
Из определения следует, что если конъюнкция
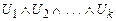 (3)
(3)
тождественно истинна, то из такой системы посылок (1) выводимы только тождественно истинные формулы, которые выводимы из любой системы посылок. Если же конъюнкция (3) тождественно ложна, то из системы посылок (1) выводима любая формула.
Если формула 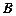 выводима из системы формул (1), то из истинности всех формул системы при некоторых значениях высказывательных переменных
выводима из системы формул (1), то из истинности всех формул системы при некоторых значениях высказывательных переменных  следует истинность формулы
следует истинность формулы 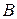 при тех же значениях переменных.
при тех же значениях переменных.
Нетрудно доказать следующие свойства выводимости.
1. Если  ú-
ú-  и
и  ú-
ú- 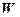 то
то  ú-
ú- 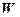 .
.
2. Если  ú-
ú-  и
и  ~
~ 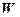 , то
, то  ú-
ú- 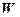 .
.
Проверка выводимости формулы 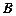 из системы посылок (1) непосредственно по определению, т.е. путем доказательства тождественной истинности формулы (2), достаточно громоздко. Рассмотрим более простой способ доказательства выводимости формулы
из системы посылок (1) непосредственно по определению, т.е. путем доказательства тождественной истинности формулы (2), достаточно громоздко. Рассмотрим более простой способ доказательства выводимости формулы 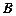 из системы посылок (1), для которых конъюнкция (3) не является ни ТИ-высказыванием, ни ТЛ-высказыванием.
из системы посылок (1), для которых конъюнкция (3) не является ни ТИ-высказыванием, ни ТЛ-высказыванием.
Теорема 7.1. Формула 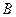 (
( 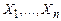 ) тогда и только тогда выводима из системы формул (1), когда все полные элементарные дизъюнкции формулы
) тогда и только тогда выводима из системы формул (1), когда все полные элементарные дизъюнкции формулы 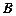 входят в СКН-форму
входят в СКН-форму  , эквивалентную формуле (3) относительно высказывательных переменных
, эквивалентную формуле (3) относительно высказывательных переменных 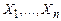 .
.
Так как теорема 1 формулирует необходимое и достаточное условие выводимости формулы, то на основе нее можно сформулировать алгоритм доказательства выводимости формулы.
1. Из системы посылок (1) строится конъюнкция (3).
2. Находим СКН-форму от высказывательных переменных для формулы (3).
3. Строим СКН-форму для формулы 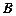 и проверяем вхождение полных элементарных дизъюнкций СКН-формы для формулы
и проверяем вхождение полных элементарных дизъюнкций СКН-формы для формулы 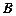 в СКН-форму для формулы (3).
в СКН-форму для формулы (3).
Задание 1. Доказать выводимость  ú-
ú- 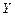 .
.
Решение.
1. Обозначим  = X,
= X,  =
= 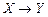 . Строим их конъюнкцию
. Строим их конъюнкцию 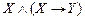 .
.
2. Найдем СКН-форму  эквивалентную этой конъюнкции.
эквивалентную этой конъюнкции.
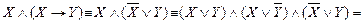 V
V
3. Получим СКН-форму для формулы B  .
.

Так как обе дизъюнкции входят в СКН-форму  , то выводимость доказана.
, то выводимость доказана.
Замечание. Выводимость формулы 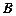 можно получить и без нахождения ее СКН-формы. Для этого нужно преобразовать с помощью известных эквивалентностей формулу (3) или даже конъюнкцию некоторых полных дизъюнкций из этой СКН-формы. Например, конъюнкция 1-ой и 3-ей полных дизъюнкций формулы
можно получить и без нахождения ее СКН-формы. Для этого нужно преобразовать с помощью известных эквивалентностей формулу (3) или даже конъюнкцию некоторых полных дизъюнкций из этой СКН-формы. Например, конъюнкция 1-ой и 3-ей полных дизъюнкций формулы  из задания 1 преобразуется с помощью формулы склеивания к искомой формуле.
из задания 1 преобразуется с помощью формулы склеивания к искомой формуле.
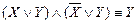
Кроме того, воспользовавшись теоремой 1, можно построить все СКН-формы выводимые из данной системы посылок. Для этого требуется небольшая модификация алгоритма доказательства выводимости формулы. После построения СКН-формы для формулы (3) необходимо
3°. Из полных элементарных дизъюнкций полученной СКН-формы строим различные комбинации конъюнкций. Эти конъюнкции и будут исчерпывать все СКН-формы, выводимые из системы посылок (1).
Дата добавления: 2016-06-13; просмотров: 1058;
