Преобразуем эту формулу, используя соответствующие эквивалентности
U º  º
º 
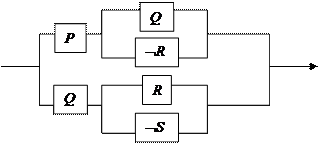
Изобразим схему, соответствующую заключительной формуле


Булевы функции
Любую формулу алгебры логики можно рассматривать как функцию, определенную на множестве B ={1, 0}.
Функцией алгебры логики (логической функцией) или булевой функцией f(x1,x2,...,xn) называетсяотображение f : B n®B, определенное на множестве упорядоченных наборов элементов множества B и принимающее значения из этого множества. Обозначим через Pn – множество булевых функций n переменных.
Логическую функцию n переменных f(x1,x2,...,xn) можно задать таблицей, в левой части которой перечислены все 2n наборов значений переменных, а в правой части – значения функции на этих наборах.
| x1 x2 . . . хn-1 xn | f(x1, x2 , . . . хn-1 , xn) |
| 0 0 . . . 0 0 0 0 . . . 0 1 0 0 . . . 1 0 . . . . . . . . . . . . . . . . 1 1 . . . 1 0 1 1 . . . 1 1 | f(0,0, . . . ,0,0) f(0,0, . . . ,0,1) f(0,0, . . . ,1,0) . . . . . . . . f(1,1, . . . ,1,0) f(1,1, . . . ,1,1) |
При любом фиксированном упорядочении наборов булева функция n переменных полностью определяется вектор-столбцом своих значений, размерность которого равна числу наборов значений функции, то есть 2n . Поэтому число различных функций n переменных равно числу различных двоичных векторов длины 2n, то есть  , т.е. |
, т.е. | 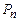 | =
| =  .
.
Нулем (единицей) булевой функции назовем упорядоченный набор значений переменных, на котором значение функции равно 0 (1).
Пусть F={ 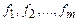 } – некоторое множество булевых функций. Его можно выбрать в качестве основного набора, называемого базисом. Формулой
} – некоторое множество булевых функций. Его можно выбрать в качестве основного набора, называемого базисом. Формулой 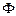 над базисом F (обозначается
над базисом F (обозначается  [F]) называется выражение вида
[F]) называется выражение вида 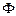 [F]=
[F]= 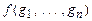 , где
, где  F, а
F, а  либо переменная, либо формула над F. Таким образом, всякая формула является суперпозицией базисных функций, для её представления обычно применяется форма записи с логическими операциями
либо переменная, либо формула над F. Таким образом, всякая формула является суперпозицией базисных функций, для её представления обычно применяется форма записи с логическими операциями 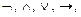 ~. Каждой формуле однозначно соответствует некоторая булева функция f, в этом случае говорят, что формула
~. Каждой формуле однозначно соответствует некоторая булева функция f, в этом случае говорят, что формула  реализует функцию f (обозначается func F = f ). Как будет показано ниже, такая реализация не единственна.
реализует функцию f (обозначается func F = f ). Как будет показано ниже, такая реализация не единственна.
Приведем примеры логических функций одной и двух переменных и их реализаций в виде формул.
Логических функций одной переменной четыре: две нуль-местные (j0(х), j3(х)) – константы 0 и 1, значения которых не зависят от значения переменной, и две одноместные функции – тождественная и отрицание.
| x | j0 | j1 | j2 | j3 |
Тождественная функция "повторяет" значение х: j1(х)=х. Функция отрицание возвращает значение, противоположное значению х: j2(х)=х.
Логических функций двух переменных шестнадцать:
| х1 | x2 | j0 | j1 | j2 | j3 | j4 | j5 | j6 | j7 | j8 | j9 | j10 | j11 | j12 | j13 | j14 | j15 |
Рассмотрим подробнее все эти функции.
* j0(х1,х2) 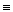 0 и j15 (х1,х2)
0 и j15 (х1,х2) 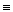 1.
1.
* j1(х1,х2) = х1 Ù х2 . Эта функция называется ещё логическим умножением и обозначается, также, х1х2.
* j2(х1.х2) = Ø (х1®х2).
* j3(х1,х2) = х1.
* j4(х1.х2) = Ø (х2®х1).
* j5(х1,х2) = х2.
* j6(х1,х2) = 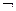 (х1~х2) называются неравнозначностью, разделительной дизъюнкцией или сложением по модулю 2 и обозначается еще как х1Å х2.
(х1~х2) называются неравнозначностью, разделительной дизъюнкцией или сложением по модулю 2 и обозначается еще как х1Å х2.
* j7(х1.х2) = х1Ú х2 .
* j8(х1.х2) = 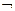 (х1Úх2) – антидизъюнкция, которая называется, также, стрелка Пирса и обозначается х1¯х2.
(х1Úх2) – антидизъюнкция, которая называется, также, стрелка Пирса и обозначается х1¯х2.
* j9(х1.х2) = х1~х2 . Эту функцию называют еще равнозначностью и обозначают х1ºх2 .
* j10(х1.х2) = 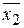 .
.
* j11(х1.х2) = х2®х1.
* j12(х1.х2) = 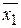 .
.
* j13(х1.х2) = х1®х2.
* j14(х1.х2) = 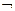 (х1Ùх2) – антиконъюнкция, которая называется еще штрих Шеффера и обозначается х1 | х2.
(х1Ùх2) – антиконъюнкция, которая называется еще штрих Шеффера и обозначается х1 | х2.
Формулы, реализующие одну и ту же функцию, называются равносильными. Отношение равносильности формул является отношением эквивалентности и обозначается º.
Фиктивной переменной (несущественной) функции f(x1, . . . , xn) называется переменная хi, изменение значения которой не меняет значения функции, то есть f(x1, . . . , хi-1, 1, xi+1, . . . , xn) = f(x1, . . . , хi-1, 0, xi+1, . . . , xn).
Например, в функциях j3 и j12 переменная х2 фиктивна, а в функциях j5 и j10 фиктивна переменная х1.
Функция f(x1, . . . , xn), имеющая фиктивную переменную xi, по существу зависит от (n–1)-й переменной, т.е. представляет собой функцию g(x1, . . . , хi-1, xi+1, . . . , xn). В этом случае говорят, что функция g получена из функции f удалением фиктивной переменной, а функция f получена из функции g введением фиктивной переменной, причём эти функции считаются равными.
Пусть f (x1, ¼ , xn) Î Pn – булева функция. Тогда функция f*(x1, ¼, xn), определенная следующим образом
f *(x1, ¼, xn) = 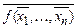 ,
,
называется двойственной к функции f.
Теорема (Принцип двойственности). Пусть F={  }. Тогда, если формула
}. Тогда, если формула 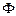 [F] реализует функцию f, то формула
[F] реализует функцию f, то формула 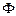 * над базисом F*={
* над базисом F*={ 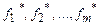 }, полученная из формулы
}, полученная из формулы 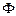 заменой функций fi на двойственные им функции fi*, реализуют функцию f *.
заменой функций fi на двойственные им функции fi*, реализуют функцию f *.
Нормальные формы
Для решения проблемы выполнимости и опровержимости формул используется специальный вид приведённых формул, называемый нормальными формами, определим их.
Элементарной конъюнкцией называется конъюнкция, в которой участвуют высказывательные переменные или их отрицания.
Элементарной дизъюнкцией называется дизъюнкция, в которой участвуют высказывательные переменные или их отрицания.
Терема 4.1. 1) Элементарная конъюнкция тождественно ложна тогда и только тогда, когда она содержит некоторую высказывательную переменную вместе с её отрицанием.
2) Элементарная дизъюнкция тождественно истинна тогда и только тогда, когда она содержит некоторую высказывательную переменную вместе с её отрицанием.
Доказательство. Докажем утверждение 1. Пусть элементарная конъюнкция тождественно ложна, предположим противное, что она не содержит никакую высказывательную переменную вместе с её отрицанием. Тогда можно построить интерпретацию, на которой эта конъюнкция истинна, придав переменным входящим в неё без отрицаний значение 1, а с отрицанием – 0. Следовательно, получено противоречие с предположением о тождественной ложности элементарной конъюнкции.
Обратное утверждение непосредственно следует из закона противоречия 9 и свойств констант 6.
Утверждение 2 доказывается аналогично.
Дизьюнктивной нормальной формой (ДНФ) называется формула, имеющая вид дизъюнкции элементарных конъюнкций.
Коньюнктивной нормальной формой (КНФ) называется формула, имеющая вид конъюнкции элементарных дизъюнкций.
Примеры.
1.  - КНФ.
- КНФ.
2. 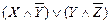 - ДНФ.
- ДНФ.
3. 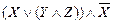 приведенная формула, но не является ни ДНФ, ни КНФ.
приведенная формула, но не является ни ДНФ, ни КНФ.
4. 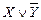 является и ДНФ, и КНФ.
является и ДНФ, и КНФ.
Теорема 4.2.Для всякой формулы U существуют эквивалентные ей КН-форма и ДН-форма.
Алгоритм построения нормальных форм.
1. Преобразовать формулу к приведенному виду (см. п.2).
2. Если полученная формула не является нормальной, то преобразовать ее к требуемой нормальной форме с помощью свойства взаимной дистрибутивности 5 операций конъюнкции и дизъюнкции.
Например ДНФ формулы примера 1 получим непосредственно по свойству 5  º
º 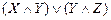 . Упростив формулу примера 3 по закону обобщенного склеивания
. Упростив формулу примера 3 по закону обобщенного склеивания 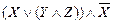 º
º 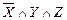 , получим КН- и ДН-форму.
, получим КН- и ДН-форму.
Задание 1.Построить нормальные формы формулы
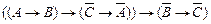 .
.
Решение. Преобразуем формулу к приведенному виду и затем упростим ее.
 º
º 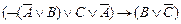 º º
º º 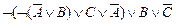 º
º  º º
º º 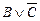
Полученная формула является КН- и ДН-формой.
ДНФ и КНФ не единственны. Существуют формулы, к которым можно привести любую логическую формулу единственным образом с точностью до порядка элементарных дизъюнкций или конъюнкций и элементов в них. Такими формулами являются совершенные нормальные формы.
Совершенной дизъюнктивной нормальной формой (СДНФ) называется ДНФ в каждой конъюнкции которой содержатся точно одно вхождение всех переменных или их отрицаний. Такие конъюнкции называются полными.
Совершенной конъюнктивной нормальной формой (СКНФ) называется КНФ в каждой дизъюнкции которой содержатся точно одно вхождение всех переменных или их отрицаний. Такие дизъюнкции называются полными.
Теорема 4.3. 1) Всякая элементарная дизъюнкция высказывательных переменных 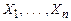 , не являющаяся ТИ-формулой, эквивалентна некоторой СКН-форме от этих высказывательных переменных.
, не являющаяся ТИ-формулой, эквивалентна некоторой СКН-форме от этих высказывательных переменных.
2) Всякая элементарная конъюнкция высказывательных переменных 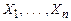 , не являющаяся ТЛ-формулой, эквивалентна некоторой СДН-форме от этих высказывательных переменных.
, не являющаяся ТЛ-формулой, эквивалентна некоторой СДН-форме от этих высказывательных переменных.
Доказательство. Докажем утверждение 1. Так как элементарная дизъюнкция не является тождественно истинной, то в силу теоремы 4.1 она не содержит никакую высказывательную переменную вместе с её отрицанием. Если некоторая переменная 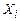 (или её отрицание
(или её отрицание 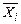 ) входит в элементарную дизъюнкцию несколько раз, то в силу идемпотентности операции дизъюнкции, оставим только одно её вхождение. Если же некоторая переменная
) входит в элементарную дизъюнкцию несколько раз, то в силу идемпотентности операции дизъюнкции, оставим только одно её вхождение. Если же некоторая переменная 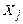 не содержится в элементарной дизъюнкции, то, воспользовавшись законом склеивания 13
не содержится в элементарной дизъюнкции, то, воспользовавшись законом склеивания 13
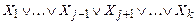 º
º 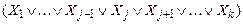 Ù
Ù
Ù 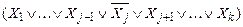 , получим КНФ. Если полученная форма не является совершенной, то для каждой её элементарной дизъюнкции повторим данную операцию. Таким образом, за конечное число применений закона склеивания получим СКНФ.
, получим КНФ. Если полученная форма не является совершенной, то для каждой её элементарной дизъюнкции повторим данную операцию. Таким образом, за конечное число применений закона склеивания получим СКНФ.
Утверждение 2 доказывается аналогично.
Следствие. Для всякой формулы, образованных из высказывательных переменных 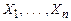 не являющейся тождественно истинной и тождественно ложной, существуют эквивалентные им СКН-форма и СДН-форма .
не являющейся тождественно истинной и тождественно ложной, существуют эквивалентные им СКН-форма и СДН-форма .
Доказательство теоремы 4.3 содержит алгоритм построения совершенных нормальных форм. Для этого нужно построить соответствующую нормальную форму, а если она не является совершенной, то расщепить конъюнкции (дизъюнкции), которые содержат не все переменные, по свойству 13.
Обе нормальные формы, построенные в задании 1, не являются совершенными. Приведем их к совершенному виду.
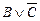 º
º 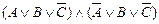 – СКН-форма.
– СКН-форма.
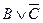 º
º  º
º
º 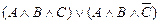 Ú
Ú 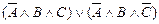 Ú
Ú
Ú 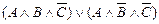 Ú
Ú 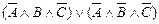 º
º
º 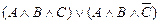 Ú
Ú 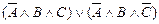 Ú
Ú 
 – СДН-форма.
– СДН-форма.
С помощью совершенных нормальных форм можно решить проблему выполнимости или опровержимости формулы.
Для того чтобы найти, при каких значениях высказывательных переменных формула является выполнимой, необходимо построить ее СДН-форму. Количество таких наборов равно числу полных элементарных конъюнкций, так как, если одна из них истинна, то истинна и вся формула. Элементарная конъюнкция истинна, когда истинны все её составляющие, следовательно, если переменная входит в неё без отрицания, то она принимает значение 1, а если с отрицанием, то – 0. Аналогично, для решения задачи опровержимости строится СКН-форма.
Сформулируем изложенные выше утверждения для булевых функций. Для этого введем следующие обозначения 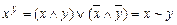 .
.
Легко проверить, что 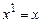 ,
, 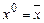 .
.
Теорема 5.4(о разложении булевых функций). Любую булеву функцию можно представить в виде
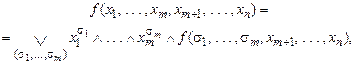 (5.1)
(5.1)
где дизъюнкции берутся по всем возможным наборам (  ).
).
Доказательство. Покажем, что правая часть равенства (5.1) совпадает с левой на произвольном фиксированном наборе значений переменных ( 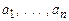 ). Подставив эти значения в левую часть (5.1), получим
). Подставив эти значения в левую часть (5.1), получим

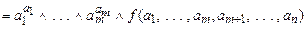 ,
,
так как, если хотя бы одно из значений 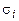 отличается от
отличается от 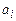 , то
, то 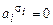 , а, следовательно, обращается в 0 и вся конъюнкция. Таким образом, отличной от 0 будет только конъюнкция на наборе (
, а, следовательно, обращается в 0 и вся конъюнкция. Таким образом, отличной от 0 будет только конъюнкция на наборе ( 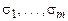 ) = (
) = ( 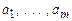 ), а так как
), а так как 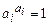 , то
, то

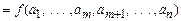 .
.
Положив в (5.1) m = n, получим
f (x1 , …, хn) = Ú (x1 ~ s1) Ù…Ù (xn ~ sn) Ù f (s1 , …, sn) .
s1,.., sn
Очевидно, среди всех дизъюнкций нужно оставить только те, в которых f (s1 , …, sn) = 1. Окончательно получим
 (5.2)
(5.2)
Полученная формула разложения является совершенной дизъюнктивной нормальной формой булевой функции.

Теорема 5.5. Всякая булева функция (кроме 0) имеет единственную СДН-форму
 .
.
С помощью принципа двойственности легко доказать представление функции СКН-формой.
Теорема 5.6. Всякая булева функция (кроме 1) имеет единственную СКН-форму
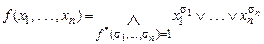 . (5.3)
. (5.3)
Совершенные нормальные формы используются также для решения задачи, обратной задаче разрешимости – построение реализации булевой функции, заданной таблицей. Нули функции определяют полные элементарные дизъюнкции, входящие в СКН-форму функции. Такая дизъюнкция строится так, чтобы все составляющие ее переменные или их отрицания обращались в нуль, т.е. если значение переменной 0, то переменная входит в дизъюнкцию без отрицания, если – 1, то – с отрицанием. Соответственно, по единицам булевой функции можно построить ее СДН-форму.
Например, функция f переменных x1, x2, x3, заданная в таблице
| x1 | x2 | x3 | f |
имеет следующие совершенные нормальные формы:
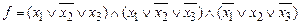 – СКН-форма;
– СКН-форма;
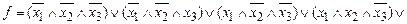
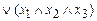 – СДН-форма.
– СДН-форма.
Упростив любую из этих формул, можно получить простейшую формулу, реализующую данную функцию.
Для вычисления значений булевых функций в общем случае надо использовать сложную рекурсивную процедуру (см. [3], п. 3.2.1.), т.к. надо определить все подформулы вплоть до Хi или 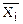 . При использовании совершенных форм алгоритм вычисления будет намного проще и эффективнее.
. При использовании совершенных форм алгоритм вычисления будет намного проще и эффективнее.
В ЭВМ совершенные формы представляются в виде матрицы размера k´n, состоящей из нулей и единиц, где k – число членов разложения (элементарных конъюнкций или дизъюнкций); n – число пропозиционных переменных. Матрица F представляет собой часть общей таблицы истинности, определяющей булеву функцию f. Для представления СДНФ берутся строки, соответствующие единицам f, а для СКНФ – строки, соответствующие нулям f.
Пусть х – массив пропозиционных переменных. Предположим, хi получили некоторые значения и необходимо вычислить значение нормальной формы f. Предлагаются следующие правила:
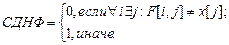
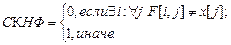
Эффективность данного алгоритма проявляется также в том, что цикл можно прервать, как только будет найдено необходимое значение i или j.
Например, вычислим значение функции f(x1, x2) = x1 ~ x2 при x1 = 0; x2 = 1. Запишем таблицу истинности функции f:
| x1 | x2 | f |
Тогда FСДНФ = 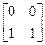 ; FСКНФ =
; FСКНФ = 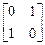 . Поскольку ни одна из строк FСДНФ, которая определяет наборы значений переменных, соответствующие 1 функции, не совпала с заданными значениями хj, то f (0, 1) = 0.
. Поскольку ни одна из строк FСДНФ, которая определяет наборы значений переменных, соответствующие 1 функции, не совпала с заданными значениями хj, то f (0, 1) = 0.
Тоже самое можно определить и по СКНФ, так как первая строка FСКНФ совпадает со значениями хj, то f (0, 1) = 0.
Определение. Булеву функцию 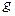 называют импликантой булевой функции
называют импликантой булевой функции 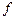 , если для любых наборов значений переменных из
, если для любых наборов значений переменных из 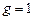 следует
следует  .
.
Если функция 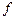 представлена ДНФ, то любая её элементарная конъюнкция будет её импликантой.
представлена ДНФ, то любая её элементарная конъюнкция будет её импликантой.
Определение. ДНФ называется минимальной, если она содержит наименьшее число вхождений переменных среди всех ДНФ, эквивалентных ей.
Определение. Длиной ДНФ называют число входящих в неё элементарных конъюнкций. ДНФ называют кратчайшей, если она имеет наименьшую длину среди всех эквивалентных ей ДНФ.
Минимальная ДНФ всегда является кратчайшей, обратное неверно.
Дата добавления: 2016-06-13; просмотров: 1174;
