Теорем и построении схем
Эквиваленция и импликация играют важную роль в математике при построении логического вывода, в частности, при доказательстве различных высказываний (теорем).
Рассмотрим, например, следующую теорему: асимметричное бинарное отношение антирефлексивно. С точки зрения алгебры высказываний теорема имеет структуру следования
А Þ В,
где А = “отношение R асимметрично”,
В = “отношение R антирефлексивно”.
Следующая теорема – для связности графа необходимо и достаточно, чтобы в нем какая-нибудь фиксированная вершина v была достижима из всех вершин, имеет вид двойного следования
А Û В (А Þ В, В Þ А),
где А = “граф G – связный”,
В = “вершина v достижима из всех вершин”.
Согласно теоремам 2.1 и 2.2, следование А Þ В имеет место тогда и только тогда, когда импликация А ® В является ТИ-формулой, а двойное следование А • В выполняется, когда ТИ-формулой является эквиваленция А ~ В. Таким образом, для доказательства какой-либо теоремы надо доказать ТИ соответствующей импликации или эквиваленции. Рассмотрим основные приемы таких доказательств, использующие законы математической логики.
Определение 1. Если А®В является истинным высказыванием, то истинность А является достаточным условием истинности В, а истинность В – необходимым условием истинности А.
Определение 2.Теоремы, записанные в виде импликаций А®В и В®А называются взаимно-обратными. Если верны обе импликации, то истинность А является необходимым и достаточным условием истинности В, и наоборот.
Определение 3.Теоремы, записанные в виде импликаций А®В и 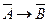 называются взаимно-противоположными.
называются взаимно-противоположными.
Предположим, что утверждение А истинно и докажем, что в этом случае В тоже истинно. Так доказывается теорема вида А ® В. Однако такая схема доказательства “в лоб” не всегда удобна. Для доказательства истинности импликаций и эквиваленций часто используют свойства эквивалентности формул.
Известно, что
А ® В º В Ú 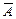 º
º 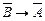 º Ø (А Ù
º Ø (А Ù 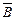 ) .
) .
Следовательно, имеем три равносильных способа доказательства, т.к. вместо истинности импликации можно доказывать истинность эквивалентной формулы.
Например, А = “отношение R асимметрично”, В = “отношение R антирефлексивно”. Тогда доказательство по схеме 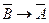 выглядит так: R рефлексивно, т.е. (х, х) Î R, значит, (х, х) Î R– 1 , т.е. (х, х) Î R È R– 1 ¹ Æ. Это означает, что R не асимметрично.
выглядит так: R рефлексивно, т.е. (х, х) Î R, значит, (х, х) Î R– 1 , т.е. (х, х) Î R È R– 1 ¹ Æ. Это означает, что R не асимметрично.
Доказательство истинности (Ø (А Ù 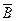 )), или, что то же самое, ложности (А Ù
)), или, что то же самое, ложности (А Ù 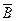 ), так называемое доказательство от противного, основано на предположении: А – истинно, а В – ложно. В результате должно быть получено ТЛ-высказывание, или противоречие.
), так называемое доказательство от противного, основано на предположении: А – истинно, а В – ложно. В результате должно быть получено ТЛ-высказывание, или противоречие.
Например, предположим, что R асимметрично и рефлексивно. В силу асимметричности неверно одно из следующих соотношений: (х, у) Î R и (у, х) Î R. Положим х = у. Тогда, включение (х, х) Î R неверно, т.е. утверждение 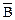 – ложно, значит и (А Ù
– ложно, значит и (А Ù 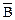 ) – ложно.
) – ложно.
В автоматическом управлении и при эксплуатации вычислительных машин приходится иметь дело с переключательными схемами (релейно-контактными, полупроводниковыми), состоящие из сотен реле, полупроводников, магнитных элементов. Переключательная схема состоит из переключателей (например, кнопочные устройства, электромагнитные реле, полупроводниковые элементы и т.п.) и соединяющих их проводников. При конструировании таких схем существенную помощь может оказать алгебра высказываний: можно построить схему, выполняющую требуемые функции (синтезирование схемы) или изучить действие построенной схемы и возможно ее упростить (анализ схемы).
Каждой схеме ставится в соответствие формула алгебры высказываний, и каждая формула реализуется с помощью некоторой схемы. Покажем, как установить такое соответствие. Каждому переключателю P ставится в соответствие высказывательная переменная P, которая истинна тогда и только тогда, когда переключатель P замкнут. Схеме с последовательным соединением переключателей P и Q соответствует формула, являющаяся конъюнкцией высказавательных переменных, соответствующих этим переключателям,  . Схеме с параллельным соединением переключателей P и Q соответствует формула, являющаяся дизъюнкцией высказавательных переменных, соответствующих этим переключателям,
. Схеме с параллельным соединением переключателей P и Q соответствует формула, являющаяся дизъюнкцией высказавательных переменных, соответствующих этим переключателям, 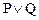 . Два переключателя P и
. Два переключателя P и 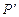 могут быть связаны так, что когда P замкнут, то
могут быть связаны так, что когда P замкнут, то 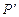 разомкнут. Тогда переключателю
разомкнут. Тогда переключателю 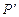 ставится в соответствие переменная
ставится в соответствие переменная 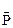 , являющаяся отрицанием P.
, являющаяся отрицанием P.
Задание. Упростить схему
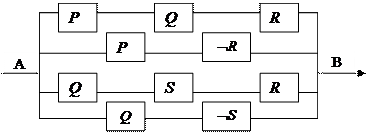
Решение. Запишем формулу, соответствующую схеме, по приведенным выше правилам
U =  .
.
Дата добавления: 2016-06-13; просмотров: 585;
