Определение. Число называется пределом последовательности , если: , такое, что выполняется: .
(для любого числа эпсилон больше нуля, существует такой номер элемента последовательности, что для всех последующих номеров отклонение элементов от числа А меньше, чем эпсилон). В этом случае говорится, что последовательность стремится к числу А.
Обозначение предела: 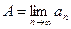 . (lim это от английского слова limit которое хорошо известно и в русском языке - лимиты потребления света, воды и т.д. ).
. (lim это от английского слова limit которое хорошо известно и в русском языке - лимиты потребления света, воды и т.д. ).
Если рассмотреть полосу от 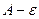 до
до 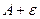 по высоте, то начиная с какого-то номера, все последующие точки будут попадать в эту полосу:
по высоте, то начиная с какого-то номера, все последующие точки будут попадать в эту полосу:
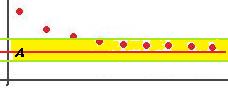
Чем меньше число 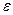 (погрешность меньше) тем больший номер требуется .
(погрешность меньше) тем больший номер требуется .
Пример. 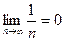 . По определению: если например требуемая точность
. По определению: если например требуемая точность  то
то 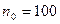 ,
, 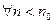 выполняется: разность элемента и 0 менее 1/100, то есть 1/101 затем 1/102 и т.д.
выполняется: разность элемента и 0 менее 1/100, то есть 1/101 затем 1/102 и т.д.
* Для того, чтобы лучше понять, что такое предел, представьте следующее. Машина приближается к городу. Для любого заранее заданного расстояния (например 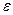 = 10 км.) существует такой момент времени
= 10 км.) существует такой момент времени 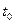 , что в последующие моменты времени
, что в последующие моменты времени 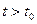 расстояние будет меньше, чем
расстояние будет меньше, чем 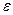 . Это как раз и означает «стремится к 0», то есть расстояние уменьшается к 0. Если задать
. Это как раз и означает «стремится к 0», то есть расстояние уменьшается к 0. Если задать 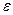 = 5 км. то это достигается в более поздний момент времени, а если
= 5 км. то это достигается в более поздний момент времени, а если 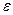 = 1 км. то ещё позже.
= 1 км. то ещё позже.
Предел может и не существовать. Для последовательности 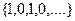 , например, предел не существует. Здесь не происходит стабилизация значений, то есть их колебания по высоте всегда 1. После каждого номера, найдётся последующий элемент, который удаляется на расстояние 1 от предыдущего, то есть эти колебания не могут быть меньше заранее заданного малого числа
, например, предел не существует. Здесь не происходит стабилизация значений, то есть их колебания по высоте всегда 1. После каждого номера, найдётся последующий элемент, который удаляется на расстояние 1 от предыдущего, то есть эти колебания не могут быть меньше заранее заданного малого числа 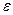 .
.
Рассмотрим последовательность 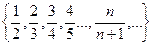
Вычислим предел. 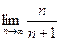 =
=  =
= 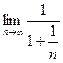 . Второе слагаемое в знаменателе стремится к 0. В итоге,
. Второе слагаемое в знаменателе стремится к 0. В итоге, 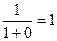 ,
, 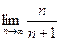 =1.
=1.
Таким же методом можно сокращать старшие степени и в других случаях, для произвольных степеней.
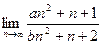 =
= 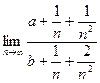 =
= 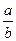 .
.
В общем случае, когда степени разные: 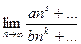 =
= 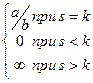 .
.
Пример. Вычислить предел 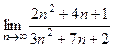
Решение.Здесь неопределённость типа  . Сократим на
. Сократим на 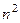 :
:
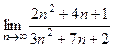 =
= 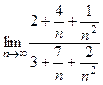 =
= 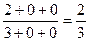 .
.
Пример. Вычислить предел 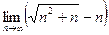 .
.
Комментарий. В выражениях с неопределённостью типа 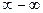 ответ не виден из самого выражения. Так, если 2 объекта от нас удаляются в бесконечность, то при этом расстояние между ними может уменьшаться, может стабилизироваться на каком-то уровне, а может возрастать. Например, для
ответ не виден из самого выражения. Так, если 2 объекта от нас удаляются в бесконечность, то при этом расстояние между ними может уменьшаться, может стабилизироваться на каком-то уровне, а может возрастать. Например, для 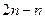 оба слагаемых стремятся к бесконечности, но и разность между ними тоже увеличивается неограниченно. А в разности
оба слагаемых стремятся к бесконечности, но и разность между ними тоже увеличивается неограниченно. А в разности  оба слагаемых увеличиваются, но разность стабильна и равна 1. Поэтому при решении таких примеров снаала нужны преобразования, приводящие к виду дроби, а там уже можно сократить на какой-то множитель.
оба слагаемых увеличиваются, но разность стабильна и равна 1. Поэтому при решении таких примеров снаала нужны преобразования, приводящие к виду дроби, а там уже можно сократить на какой-то множитель.
Итак, 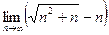 умножим на сопряжённое выражение, то есть на сумму, подобную этой разности. Тогда можно будет применить формулу сокращённого умножения, и корень исчезнет, так как он будет возведён в квадрат.
умножим на сопряжённое выражение, то есть на сумму, подобную этой разности. Тогда можно будет применить формулу сокращённого умножения, и корень исчезнет, так как он будет возведён в квадрат.
= 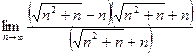 =
= 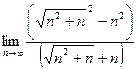 =
=  =
= 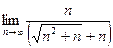
В знаменателе содержится n и выражение, содержащее корень из 2 степени, которое по скорости роста сопоставимо с n. Сократим числитель и знаменатель на n.
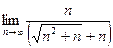 =
= 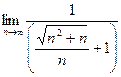 =
= 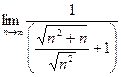 =
= 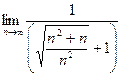 . Чтобы разделить корень, удобно факт деления на n представили как деление на корень из n2, продолжим:
. Чтобы разделить корень, удобно факт деления на n представили как деление на корень из n2, продолжим:
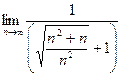 =
= 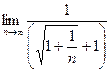 =
= 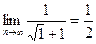 .
.
Вычислительный эксперимент. Чтобы луше понять понятие предела, можете вычислить выражение 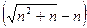 например, при n = 100, n = 1000 на калькуляторе. Чем больше n тем ближе к 0,5 ответ получится.
например, при n = 100, n = 1000 на калькуляторе. Чем больше n тем ближе к 0,5 ответ получится.
n = 100 результат 0,49876. Отклонение от 1/2 составило 0,00124.
n = 1000 результат 0,49988. Отклонение от 1/2 составило 0,00012.
Теорема 1. Пусть дано 3 последовательности, причём для любого номера n: 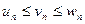 . Если
. Если 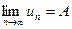 ,
, 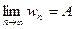
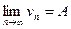 .
.
Доказательство. Так как для первой и третьей последовательности предел равен А, то числа 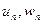 (начиная с какого-то номера) отклоняются от
(начиная с какого-то номера) отклоняются от 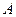 не больше чем на величину
не больше чем на величину 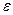 , то есть принадлежат интервалу
, то есть принадлежат интервалу 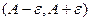 . Но число
. Но число 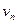 находится между ними, тогда оно тоже принадлежит
находится между ними, тогда оно тоже принадлежит 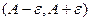 . Тогда по определению, для средней последовательности тоже существует предел.
. Тогда по определению, для средней последовательности тоже существует предел.
Теорема 2. Если последовательность монотонно возрастает (убывает) и ограничена сверху (снизу), то она имеет конечный предел.
Примеры нарушения одного из этих двух условий.
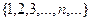 не ограничена, предел
не ограничена, предел 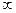 .
.
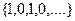 не монотонна. Пределом не может быть ни одно из чисел 0 или 1. Здесь после любого элемента, среди последующих есть какой-либо, удалённый от данного на расстояние 1, то есть в определении предела было бы не «для любого
не монотонна. Пределом не может быть ни одно из чисел 0 или 1. Здесь после любого элемента, среди последующих есть какой-либо, удалённый от данного на расстояние 1, то есть в определении предела было бы не «для любого 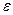 », а только для
», а только для 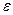 >1. Колебания по высоте не уменьшаются, все последующие элементы не впишутся в узкую полосу ширины
>1. Колебания по высоте не уменьшаются, все последующие элементы не впишутся в узкую полосу ширины 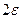 .
.
Дата добавления: 2016-12-26; просмотров: 781;
