Множества на действительной оси.
Основы математического анализа.
Множества и функции.
Множеством называют совокупность объектов некоторого типа. Например, множество точек на плоскости, множество чисел, множество матриц.
Объединение 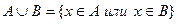
Пересечение 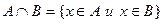
Объединение и пересечение 2 множеств показаны графически:
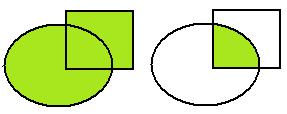
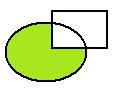
Разность множеств: 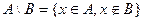 . Показано на чертеже:
. Показано на чертеже:
Аналогично, 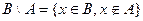 .
.
Объединение этих двух разностей называется симметрической разностью, и обозначается так: 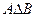 =
= 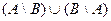 , на чертеже:
, на чертеже:
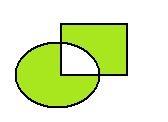
В то же время, это множество можно получить и другим путём: из объединения удалить пересечение. То есть,
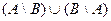 =
= 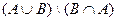 .
.
Ещё обозначения: 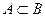 - множество А является подмножеством множества В.
- множество А является подмножеством множества В.
Числовые множества.
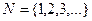 натуральные числа
натуральные числа
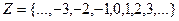 целые числа
целые числа
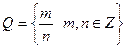 рациональные числа
рациональные числа
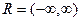 вся действительная ось, действительные числа.
вся действительная ось, действительные числа.
Множество 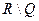 - иррациональные числа.
- иррациональные числа.
Верно следующее: 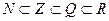 .
.
Существует обобщение: комплексные числа вида 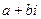 . Комплексная плоскость.
. Комплексная плоскость.
Множества на действительной оси.
Интервал 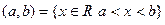 - граничные точки не включены.
- граничные точки не включены.
Отрезок 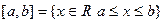 - здесь границы включены во множество.
- здесь границы включены во множество.
Пример. Найти объединение и пересечение множеств 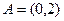 ,
, 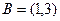
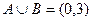
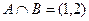 .
.
Множество вида 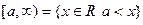 . Числа «бесконечность» не существует, поэтому в таком множестве справа всегда должна быть круглая скобка.
. Числа «бесконечность» не существует, поэтому в таком множестве справа всегда должна быть круглая скобка.
Интервал вида 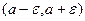 в будущем будем называть окрестностью радиуса
в будущем будем называть окрестностью радиуса 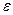 точки
точки 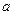 и обозначать
и обозначать 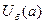 .
.
Дата добавления: 2016-12-26; просмотров: 599;
