Определение. Число называется пределом функции в точке , если: , такое, что при выполняется: .

(для любого числа эпсилон больше нуля, существует такое число дельта, так что если модуль разности 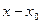меньше дельта, то модуль разности 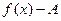меньше, чем эпсилон).

Обозначение .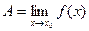

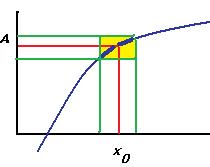
В случае существования предела, получается, что задавая погрешность 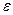можно найти такой интервал в области определения, что отклонение значений от А будет меньше чем 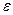. Фактически, часть графика впишется в некоторый прямоугольник, при уменьшении одной стороны будет уменьшаться и вторая.

У студентов может закономерно возникнуть вопрос, а для чего вообще нужно понятие предела в точке, и почему нельзя просто подставить 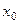и вычислить функцию. Проблема в том, что не всегда значение функции существует в точке. Иногда бывает так, что формально её вычислить нельзя. Например, для функции 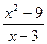значение в точке 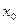=3 не существует. При вычислении на калькуляторе поочерёдно числителя и знаменателя, получили бы 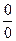и калькуляторы, компьютеры выдали бы сообщение об ошибке. Но ведь в соседних точках значение функции есть. График функции подходит к некоторой точке в плоскости. Так вот, её ордината и равна этому пределу.

Пример. Вычислить предел .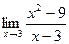

В точке 3 значение функции не существует, однако во всех соседних точках существует, и можно узнать, к какой ординате стремится график при . Разложим на множители:

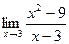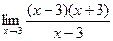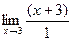= = = 6.

Тот множитель, который отвечал за стремление к 0 в числителе и знаменателе, сокращён, поэтому далее удалось просто подставить 3 и получить ответ.

Как видим, методы разные: если неопределённость типа 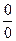, то выделяем множители, чтобы сократить те множители, которые стремятся к 0. Если неопределённость , то корни искать не нужно, а нужно сократить на степенную функцию старшей степени. Для неопределённостей типа 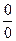основным методом является разложение на множители, и сокращение тех множителей, которые ответственны за стремление к 0.

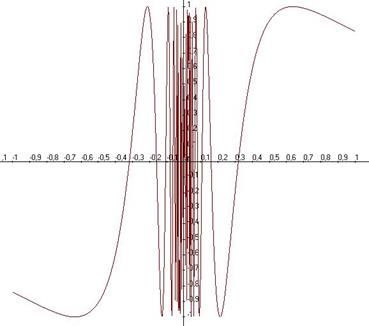
Пример функции, не имеющей предела в нуле. 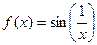. Здесь при приближении к 0 бесконечное число колебаний, то есть, уменьшая область определения, например интервал 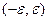, никак не удастся получить уменьшение области значений функции над этим интервалом, размах колебаний всё равно останется от -1 до 1. При подходе абсциссы к 0, функция здесь должна пройти бесконечное число колебаний амплитуды 2 (от -1 до 1).

Лекция № 10. 11. 11. 2016

Метод Лопиталя для неопределённостей 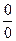. Несмотря на то, что тема «производные» подробно будет позже, и доказательство этого метода будет дано в той теме, производные для некоторых элементарных функций известны из школы, и можно этим пользоваться при вычислении пределов.

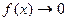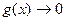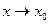Если , при и ,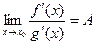

то .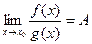

Пример. = = = .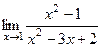

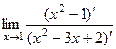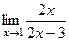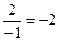Этот метод можно применять и в 2 или более шагов, если после 1-го дифференцирования остаётся неопределённость .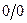

Вычислим этим же способом 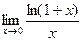= = 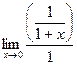1.

График ln(1+x) это ln(x) сдвинутый влево на 1, касательная проходит ровно под углом 45 градусов, то есть совпадает с функцияей y = x. Если рассмотреть при большом увеличении, они почти неотличимы.

Ещё пример. .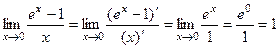

Ещё пример. .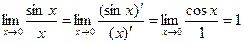

1-й замечательный предел. .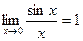

Доказательство 1-го замечательного предела из геометрических соображений.

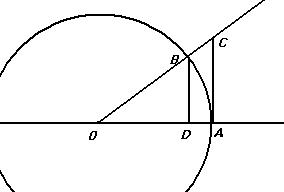
Рассмотрим единичную окружность, и какой-либо угол. Длина дуги AB равна 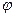- это по определению радианной меры угла. Так как ОА это радиус, а мы взяли единичную окружность, то

.

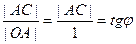Так как ОВ это тоже радиус, то .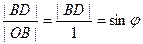

Но длина дуги на чертеже больше, чем отрезок BD, и меньше, чем AC.

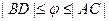, то есть .

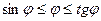Совпадают они именно при .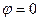

Кстати, графики трёх функций именно так и расположены: у них общая касательная, тангенс выше, синус ниже, чем биссектриса.

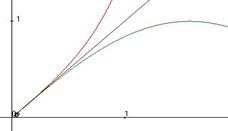
Неравенства 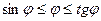перепишем в виде: .

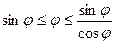Теперь разделим всё на синус. 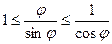. Рассмотрим обратные величины ко всем этим, пользуясь тем, что из 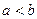следует 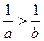. Получится .

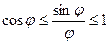Применим свойство, которое доказывали когда-то ранее: если 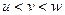и две крайние из 3 величин стремятся к А, то и средняя имеет предел и стремится к А.

Учитывая, что 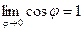, а константа справа и так равна 1, то .

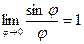Если обозначение угла сменить, обозначить x, то и получается .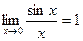

Следствия из 1-го замечательного предела:

, , , .

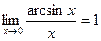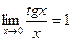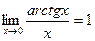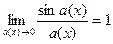Пример. .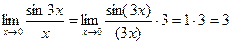

Более подробно: мы могли бы заменить 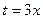, и учесть, что при 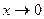будет и .

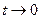Пример. Найти предел .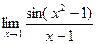

Решение. Надо получить в знаменателе такое же выражение, как под знаком sin.

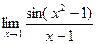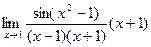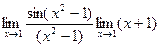= = = 2.

Здесь можно в процессе решения переобозначить 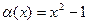, причём 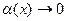при .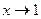

2-й замечательный предел.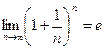

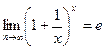
Обратите внимание, что этот предел вовсе не 1, как могло бы показаться. Ведь в степень всегда возводится не 1, а число, большее, чем 1. Оно уменьшается, но оно ни при каком n не равно 1. Здесь 2 процесса: одновременно уменьшается основание до единицы, и при этом увеличивается степень. Всё зависит от соотношения скоростей этих процессов.

Если, к примеру, есть 2 процесса: растворение краски и замораживание ёмкости с водой, то существенно отличается результат, если выполнить 1-й или 2-й процесс раньше. Если сначала заморозить воду, то уже ничего не растворится, а если сначала растворить, то будет равномерная смесь. Если замораживать одновременно с растворением, то будет другой результат, краска растворится не равномерно. Короче говоря, мы не имеем права считать, что сначала уменьшили основание в выражении 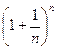и только потом стали увеличивать степень, здесь оба процесса идут одновременно, поэтому сказать, что такой предел всегда равен 1, будет ошибкой.

Число, даже очень близкое к 1, при возведении в выокую степень существенно возрастает. Так, при инфляции 10% в год, за 20 лет цена будет почти в 7 раз больше: 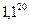= 6,7275. А если 15% в год, то за 20 лет в 16 раз больше: 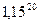= 16,36654.

Докажем, используя некоторые ранее полученные пределы, чтобы понять, каким образом в этом пределе появляется число e.

Возьмём выражение 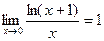, запишем как 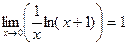.По свойству логарифма, 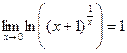. Возведём в степень e:

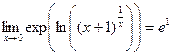, то есть .

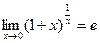Если ввести замену 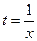, то получим 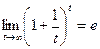. Если здесь выбрать значения только для целых абсцисс, то получится .

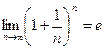Следствия из 2-го замечательного предела.

, , , .

Вообще, с помощью 2 замечательного предела можно раскрывать неопределённости вида .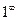

Пример. Вычислить предел .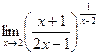

Решение. Заметим, что если отдельно рассмотреть основание, видно, что оно стремится к 1 (там получается 3/3). Степень стремится к бесконечности. Таким образом, здесь есть неопределённость вида 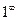, и можно применять 2-й замечательный предел.

Выделим целую часть этой неправильно дроби. Это можно сделать так: вписать перед дробью +1, а после неё (-1). Затем привести к общему знаменателю всё, что после первой единицы, то есть второй и третий элементы.

= =

= .

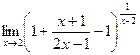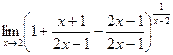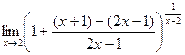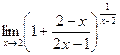Обратите внимание, что само собой автоматически получилось, что после 1 такая дробь, которая стремится к 0. Это и должно было получиться, ведь всё основание стремится к 1. Теперь нужно в степени искусственно домножить на дробь, обратную к той, что в основании следует после единицы. Но чтобы степень в примере не изменилась, надо компенсировать домножением и на саму эту дробь, а не только на обратную.

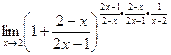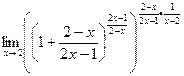= В больших скобках получилось выражение типа 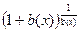, его предел равен e. Таким образом,

осталось найти = = = .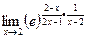

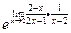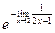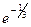Чтобы степени было видно крупнее, можно записать через exp(A) вместо e^A.

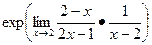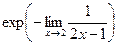= . Итак, .

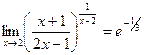* Замечание. Если основание стремится не к 1, а к другому числу, то второй замечательный предел можно и не использовать. Так, если 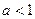то предел равен 0, если 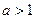то .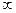

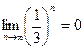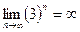, . Неопределённость возникает только в том случае, когда основание стремится к 1.