Вопрос 2. Кривая LM как характеристика множества равновесных состояний на рынке денег

Деньги – наиболее ликвидный, но наименее доходный актив. Поэтому существует оптимальное количество денег, которое хотят иметь экономические субъекты. Оно называется спросом на деньги. Спрос на деньги имеет две составляющие. Трансакционный спрос на деньги (спрос на деньги для сделок) находится в прямой зависимости от уровня дохода:

L_сд = L(y) или L_сд = K*P*Y,

где L_сд – трансакционный спрос на деньги,

P – уровень цен;

у – доход;

К – коэффициент ликвидности, отражающий долю дохода, которую экономические субъекты хотят иметь на руках, в наличной форме.

Спекулятивный спрос на деньги (спрос на деньги как на имущество) зависит от привлекательности альтернативных видов имущества, прежде всего облигаций. Поэтому с ростом ставки процента он уменьшается:

L_им = L(i),

где L_им – спекулятивный спрос на деньги.

Предложение денег задается государством.

Денежный рынок находится в состоянии равновесия, когда денежный спрос равен денежному предложению:

M = L_им (i) + L_сд (y),

где М – предложение денег.

II квадрант – кривая, отражающая обратную зави-симость L_им и i;

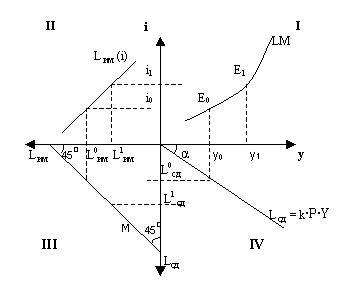III квадрант – вспомо-гательная линия, обра-зующая с осями координат углы в 45˚. Она показывает распре-деление денежной массы на L_им и L_сд. Удаление линии от начала координат составляет величину денежной массы – М. IV квадрант – линия, отражающая прямую зависимость L_сд и у, при этом K = tgα. I квадрант – построение линии LM.

Рис. 15.2. Построение линии LM

Если процентная ставка установится на уровне i₀, тогда спрос на деньги как на имущество составит L⁰_им. При заданном предложении денег М равновесие будет обеспечено, если оставшаяся часть денежного предложения будет востребована трансакционным спросом на деньги L_сд⁰. А это возможно при уровне дохода у₀. Паре равновесных значений i₀ и у₀ соответствует точка Е₀. Ход размышлений можно повторить, получив точки Е₁ и Е₂ и т. д. Соединив данные точки, получим линию LM (от англ. liquidity preference - money – предпочтение ликвидности - деньги).

Каждая точка кривой LM отражает соотношения процентной ставки и дохода, при которых на денежном рынке достигается равновесие. Все точки, находящиеся правее или левее линии LM, отражают, соответственно, ситуации дефицита или избытка денег.

Положительный наклон линии LM объясняется тем, что при заданном предложении денег рост национального дохода вызывает рост трансакционного спроса на деньги. Следовательно, для сохранения равновесия необходимо сокращение спекулятивного спроса на деньги, что возможно при повышении процентной ставки. Таким образом, более высокий доход ведет к более высокой ставке процента.

Конфигурация линии LM позволяет выделить на ней три ярко выраженных участка: горизонтальный, промежуточный и вертикальный. Это объясняется характером кривой 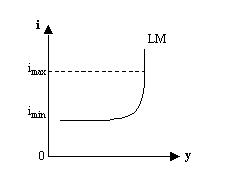спекулятивного спроса на деньги: при приближении ставки процента к i_max число людей, предъявляющих спрос на деньги как на имущество резко уменьшается, соответственно эластичность спекулятивного спроса по ставке процента снижается.

Рис. 15.3. Линия LM

Если процентная ставка превысит значение i_max, то никто не будет держать свои сбережения в денежной форме, а обратит их в ценные бумаги. Т.е. на вертикальном отрезке линии LM равновесие денежного рынка определяется лишь трансакционным спросом, который не зависит от ставки процента.

Если спекулятивный спрос на деньги очень чувствителен к ставке процента, то кривая LM почти горизонтальна. При приближении процентной ставки к значению i_min число людей, предъявляющих спрос на деньги как на имущество, резко сокращается. Если процентная ставка достигнет значения i_min, то экономические субъекты переведут все свои сбережения в наличную форму. Если меняется количество денег, находящихся в обращении, то происходит сдвиг линии LM: вправо – при увеличении, влево – при уменьшении.