Пример 5.2. Автокорреляционная функция и выявление структуры ряда.

Пусть имеются условные данные об объемах потребления электроэнергии жителями региона за 16 кварталов (табл.5.3).

Таблица 5.3

Потребление электроэнергии жителями региона, млн кВт . ч

t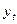
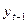
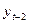
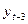
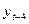
1 6,0 - - - - 2 4,4 6,0 - - - 3 5,0 4,4 6,0 - - 4 9,0 5,0 4,4 6,0 - 5 7,2 9,0 5,0 4,4 6,0 6 4,8 7,2 9,0 5,0 4,4 7 6,0 4,8 7,2 9,0 5,0 8 10,0 6,0 4,8 7,2 9,0 9 8,0 10,0 6,0 4,8 7,2 10 5,6 8,0 10,0 6,0 4,8 11 6,4 5,6 8,0 10,0 6,0 12 11,0 6,4 5,6 8,0 10,0 13 9,0 11,0 6,4 5,6 8,0 14 6,6 9,0 11,0 6,4 5,6 15 7,0 6,6 9,0 11,0 6,4 16 10,8 7,0 6,6 9,0 11,0

Нанесем эти значения на график (рис.5.2).

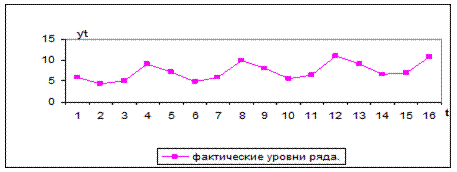
Рис 5.2. потребления электроэнергии жителями региона.

Определим коэффициент автокорреляции первого порядка (добавим 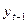в табл. 5.3 и воспользуемся формулой расчета линейного коэффициента корреляции). Он составит: r₁ = 0,165. Отметим, что расчет этого коэффициента производился по 15, а не по 16 парам наблюдений. Это значение свидетельствует о слабой зависимости текущих уровней. 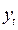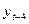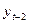Однако, как следует из графика, структура этого такова, что каждый следующий уровень от уровня и в гораздо большей степени, чем от уровня 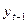. Построим ряд 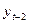(см. табл. 5.3 ). Рассчитав коэффициент автокорреляции второго порядка r₂, получим количественную характеристики корреляционной связи рядов 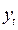, , 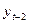r₂ = 0,567 _. Продолжив расчеты аналогичным образом, получим автокорреляционную функцию этого ряда. Ее значение и коррелограмма приведены в табл. 5.4.

Табл.5.4