Уравнения трендов для временного ряда темпов роста номинальной месячной заработной платы за 10 месяцев 1999 г., % к уровню декабря 1998 г.

Тип тренда	Уравнение	R2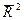
Линейный	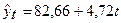(0,595)	0,887	0,873
Парабола второго порядка	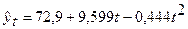(2,11) (0,187)	0,937	0,920
Степенной	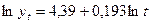(0,017)	0,939	0,931
Экспоненциальный	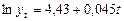(0,006)	0,872	0,856
Гиперболический	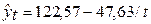(0,8291)	0,758	0,728

Наиболее простую экономическую интерпретацию имеют параметры линейного и экспоненциального трендов.

Параметры линейного тренда можно интерпретировать так:

a - начальный уровень временного ряда в момент времени t = 0

b – средний за период абсолютный прирост уровней ряда. Применительно к данному временному заработной платы за 10 месяцев 1999 г. изменились от уровня 82,66% со средним за месяц абсолютным приростом, равным 4б72 проц. пункта. Расчетные по линейному тренду значения уровней временного ряда определяются двумя способами. Во- первых, можно последовательно подставлять в найденное уравнение тренда значения t = 1,2,….,n т.е.

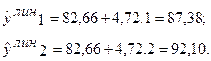
Во- вторых, в соответствии с интерпретацией параметров линейного тренда каждый последующий уровень ряда сумма предыдущего уровня и среднего цепного абсолютного прироста, т.е.

и т.д.

График линейного тренда приведен рис 5.3.

Параметры экспоненциального тренда имеют следующую интерпретацию. Параметр a – это начальный уровень временного ряда в момент времени t = 0. Величина e^b – это средний за единицу времени коэффициент роста уровней ряда.

Для нашего примера уравнение экспоненциального тренда в исходной форме имеет вид:

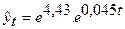
или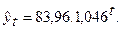

Таким образом, начальный уровень ряда в соответствии с уравнением экспоненциального тренда составляет 83,96 (сравните с начальным уровнем 82,66 в линейном тренде), а средний цепной коэффициент роста – 1,046. Следовательно, можно сказать, что темпы роста номинальной месячной заработной платы за 10 месяцев 1999г. изменялись от уровня 83,96% со средним за месяц цепным темпом роста, равным 104,6%. Иными словами, средний за месяц цепной темп прироста временного ряда составил 4.6%.

По аналогии с линейной моделью расчетные значения уровней ряда по экспоненциальному тренду можно получить как путем подстановки в уравнение тренда значений t = 1,2,….,n, так и в соответствии с интерпретацией параметров экспоненциального тренда: каждый его последующий уровень есть произведение предыдущего уровня на соответствующий коэффициент роста.

При наличии неявной нелинейной тенденции следует дополнять описанные выше методы выбора наилучшего уравнения тренда качественным анализом динамики изучаемого показателя, с тем чтобы избежать ошибок спецификации при выборе вида тренда. Качественный анализ предполагает изучение проблем возможного наличия в исследуемом временном ряде поворотных точек и изменения темпов прироста, или ускорения темпов прироста, начиная с определенного момента (периода) времени под влиянием ряда факторов, и т.д. В случае если уравнение тренда выбрано неверно при больших значениях t, результаты анализа и прогнозирования динамики временного ряда с использованием выбранного уравнения будут недостоверными вследствие ошибки спецификации.

Иллюстрация возможного появления ошибки спецификации приводится на рис. 5.4.

Рис. 5.4. ошибка спецификации при выборе уравнения тренда

Если наилучшей формой тренда является парабола второго порядка, в то время как на самом деле имеет место линейная тенденция, то при больших t парабола и линейная функция будут по разному описывать тенденцию в уровнях ряда. При t> t* парабола второго порядка характеризует убывающую тенденцию в уровнях ряда yt, а линейная функция - возрастающую.