Расчет выровненных значений Т и ошибок Е в аддитивной модели

t	Yt	Si	T+E = Yt- Si	T	T+S	E = Yt – (T+S)	E²

		0,581	5,419	5,902	6,483	-0,483	0,2333
	4,4	-1,977	6,377	6,088	4,111	0,289	0,0835
		-1,294	6,294	6,275	4,981	0,019	0,0004
		2,69	6,31	6,461	9,151	-0,151	0,0228
	7,2	0,581	6,619	6,648	7,229	-0,029	0,0008
	4,8	-1,977	6,777	6,834	4,857	-0,057	0,0032
		-1,294	7,294	7,02	5,726	0,274	0,0751
		2,69	7,31	7,207	9,897	0,103	0,0106
		0,581	7,419	7,393	7,974	0,026	0,0007
	5,6	-1,977	7,577	7,58	5,603	-0,003	0,0009
	6,4	-1,294	7,694	7,766	6,472	-0,072	0,0052
		2,69	8,31	7,952	10,642	0,358	0,1282
		0,581	8,419	8,139	8,72	0,28	0,0784
	6,6	-1,977	8,577	8,325	6,348	0,252	0,0635
		-1,294	8,294	8,519	7,225	-0,225	0,0506
	10,8	2,69	8,11	8,698	11,388	-0,588	0,3457

Шаг 4.Определим компоненту Т данной модели. Для этого проведем аналитическое выравнивание ряда (Т+Е) с помощью линейного тренда. Результаты аналитического выравнивания следующие:

Константа 5,715416

коэффициент регрессии 0,186421

стандартная ошибка коэффициента регрессии 0,015188

R – квадрат 0,914971

число наблюдений 16

число степеней свободы 14

Таким образом, имеем следующий линейный тренд:

Т = 5,715+0,186t

Поставляя в это уравнение значения t = 1, …..16, найдем уровни Т для каждого момента времени (гр.5 табл. 5.10.). График уравнения тренда приведен на рис.5.5

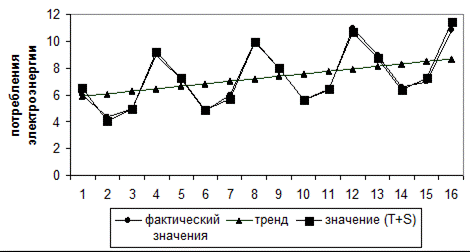
Рис. 5.5. потребления электроэнергии жителями района (фактические, выровненные и полученные по аддитивной модели значения уровней ряда.)

Шаг 5.Найдем значенияуровней ряда,полученные по аддитивной модели. Для этого прибавим к уровням Т значения сезонной компоненты для соответствующих кварталов. Графически значения (Т+S) представлены на рис 5.5.

Шаг 6. В соответствии с методикой построения аддитивной модели расчет ошибки производится по формуле:

E = Yt – (T+S) (5.8)

Это абсолютная ошибка. Численные значения абсолютных ошибок приведены в гр.7 табл.5.10.

По аналогии с моделью регрессии для оценки качества построения модели или для выбора наилучшей модели можно применять сумму квадратов полученных абсолютных ошибок. Для данной аддитивной модели сумма квадратов полученных абсолютных ошибок равна 1,1. По отношению к общей сумме квадратов отклонений уровней ряда от его средней уровня, равной 71,59, эта величина составляет чуть более 1,5%:

(1-1,1/71,59)* 100 = 1,536

Следовательно, можно сказать, что аддитивная модель объясняет 98,5% общей вариации уровней временного ряда потребления электроэнергии за последние 16 кварталов.

Пример 5.5. Построение мультипликативной модели временного ряда .

Пусть имеются поквартальные данные о прибыли компании за последние 4 года (табл. 5.11)

Таблица 5.11.

<38 39 404142 43 44 >

Дата добавления: 2016-05-16; просмотров: 1904;