Применение фиктивных переменных для моделирования сезонных колебаний.

Рассмотрим еще один метод моделирования временного ряда, содержащего сезонные колебания, - построение модели регрессии с включением фактора времени и фиктивных переменных. Количество фиктивных переменных в такой модели должно быть на единицу меньше числа моментов (периодов) времени внутри одного цикла колебаний. Например, при моделировании поквартальных данных модель должна включать 4 независимые переменные. Каждая фиктивная переменная отражает сезонную (циклическую) компоненту временного ряда для какого-либо одного периода. Она равна единице для данного периода и нулю для всех остальных периодов.

Пусть имеется временной ряд, содержащий циклические колебания периодичностью к. Модель регрессии с фиктивными переменными для этого ряда будет иметь вид:

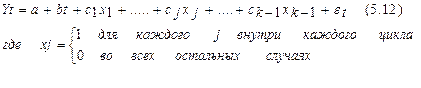
Например, при моделировании сезонных колебаний на основе поквартальных данных за несколько лет число кварталов внутри одного года к=4, а общий вид модели следующий:

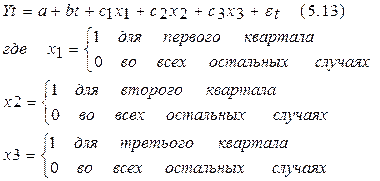
Уравнение тренда для каждого квартала будет иметь следующий вид:

для I квартала: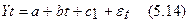

для II квартала:

для III квартала: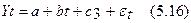

для IV квартала: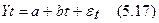

Таким образом, фиктивные переменные позволяют дифференцировать величину свободного члена уравнения регрессии для каждого квартала. Она составит:

для I квартала: а+с1

для II квартала: а+с2

для III квартала: а+с3

для IV квартала: а

Параметр b в этой модели характеризует среднее абсолютное изменение уровней ряда под воздействием тенденции. В сущности, модель (5.13) есть аналог аддитивной модели временного ряда, поскольку фактический уровень временного ряда есть сумма трендовой, сезонной и случайной компонент.