Расчетные данные для второго шага ДМНК
| х1 | х2 | 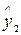
| 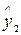 +х1=z +х1=z
| у1 | y1z | z2 |
| -1,4 | -0,4 | 0,103 | -1,297 | -2 | 2,594 | 1,682 |
| -0,4 | -2,4 | 0,042 | -0,358 | -1 | 0,358 | 0,128 |
| 0,6 | -1,4 | -0,035 | 0,565 | 0,319 | ||
| -0,4 | 1,6 | 0,020 | -0,380 | -0,380 | 0,144 | |
| 1,6 | 2,6 | -0,130 | 1,470 | 2,940 | 2,161 | |
| å0 | 5,512 | 4,434 |
После того как найденной оценки эндогенной переменной у2, обратимся к сверхидетифицируемому структурному уравнению
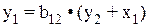 .
.
Заменяя фактические значения у2 их оценками 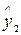 , найдем значения новой переменной
, найдем значения новой переменной
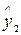 + х1 = z.
+ х1 = z.
Далее применяем МНК к уравнению
 ,
,
т.е. 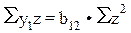 .
.
Откуда 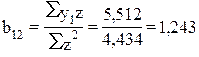 .
.
Таким образом, сверхидетифицируемое структурное уравнение составит:
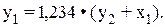 .
.
Ввиду того, что второе уравнение нашей системы не изменилось, то ее структурная форма, найденная из системы приведенных уравнений, та же:
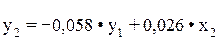 .
.
В целом рассматриваемая система одновременных уравнений составит:


ДМНК является наиболее общим и широко распространенным методом решения системы одновременных уравнений. Для точно идентифицируемых уравнений ДМНК дает тот же результат, что и КМНК. Поэтому в ряде компьютерных программ, например DSTAT, для решения системы одновременных уравнений рассматривается лишь ДМНК.
Решение сверхидентифицируемой системы на компьютере построено на предположении, что при каждой переменной в правой части системы имеется свой структурный коэффициент. Если же в модель вводятся ограничения на параметры, как в рассмотренном примере b12 = a21, то программа DSTAT не работает. Структурная модель может принимать любой вид, но без ограничений на параметры. При этом должно выполняться счетное правило идентификации: D + 1 > H.
Дата добавления: 2016-05-16; просмотров: 686;
